4.2 — An Economic Model of Precaution
ECON 315 • Economics of the Law • Spring 2021
Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/lawS21
lawS21.classes.ryansafner.com
Precaution: An Economic Model
Precaution
As usual, our main concern is with the incentives these various liability rules create
For torts, focus on parties' incentive to invest in (costly) precaution to avoid accidents
- Driving/bicyling carefully, installing seatbelts, airbags, wearing helmets, etc.
- Inspecting products carefully, quality control, independent audits, mandatory work breaks
- All of these things are costly to parties, so there must be some efficient level

Precaution
- Actions by both injurer and victim impact the number of accidents
- Speed like hell, drive drunk, texting
- Bicycle in the dark wearing black, no helmet
- Manufacture cheap, shoddy product quickly
- Drive slowly and soberly
- Bicycle wearing helmet and reflectors
- Manufacture slow, quality controlled & inspected product

Precaution
- Actions by both injurer and victim impact the number of accidents
- Speed like hell, drive drunk, texting
- Bicycle in the dark wearing black, no helmet
- Manufacture cheap, shoddy product quickly
- Drive slowly and soberly
- Bicycle wearing helmet and reflectors
- Manufacture slow, quality controlled & inspected product

Precaution: any activity either party can do to reduce probability of an accident (or severity of damage)
How much precaution is efficient?
How do we design the law to get this amount?
A Simple Economic Model of Accidents
Our main example was a car hitting a bicyclist, in real life:
- Driver probably has insurance
- Some damage to bicycle and to driver’s car
- Driver and bicyclist may not even know what the law is
We will simplify a lot by assuming:
- Only one party is harmed
- Parties know the law
- Parties don’t have any insurance (for now)
- Focus only on one party’s precaution at a time

A Unilateral Care Model
Unilateral harm (just one victim)
Precaution: costly actions that make accident less likely
- Could be taken by either victim or injurer
- We'll consider both, but one at a time

A Unilateral Care Model: Definitions/Notation
x: amount of precaution taken
w: cost of each “unit” or precaution
- total cost of precaution is wx
p(x): probability of an accident, given level of x
- ∂p(x)∂x<0
A: cost of accident (to victim)
- expected cost of accidents is p(x)A
When we examine injurer we will use x, when we examine victim we will use y
- Your textbook uses xi and xv

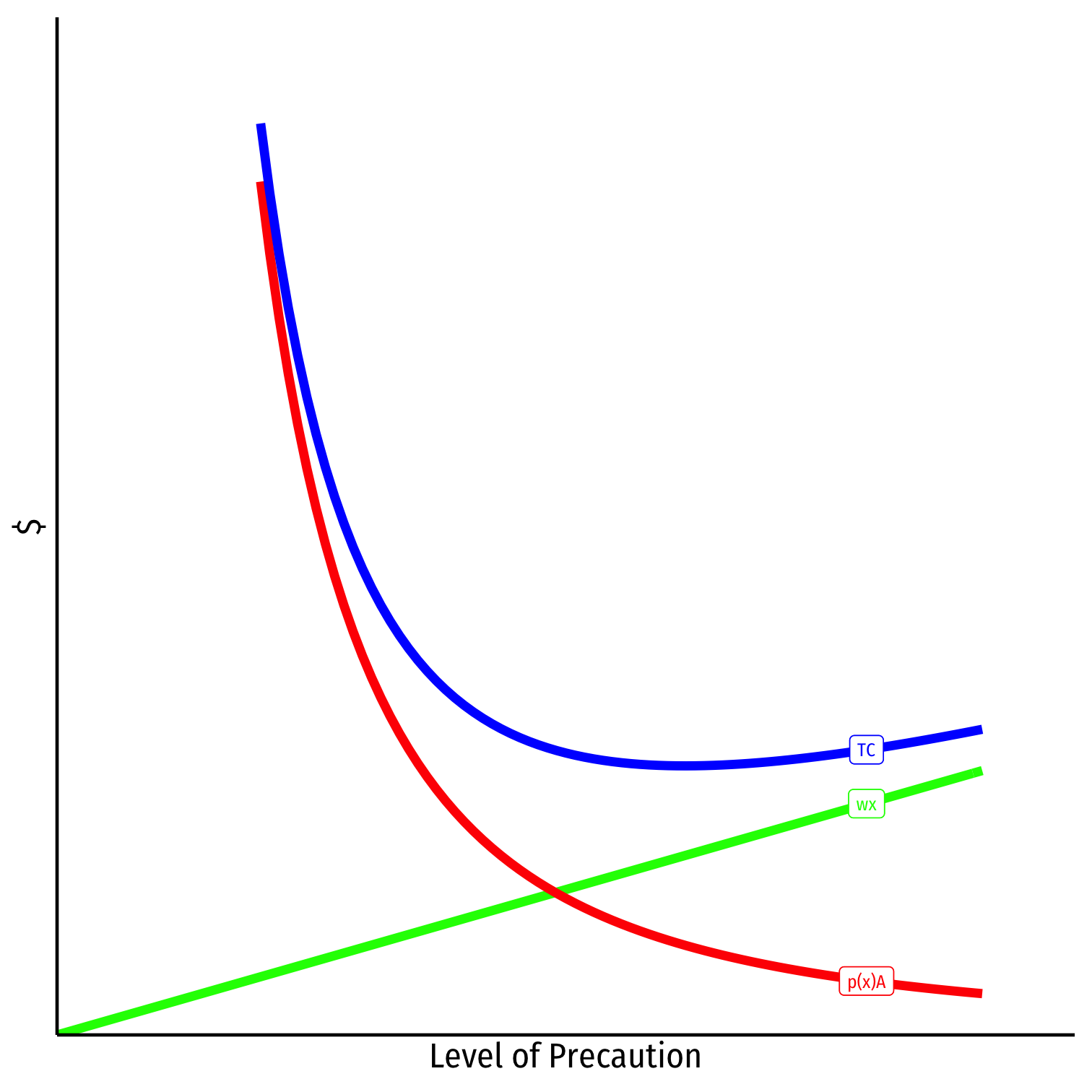
A Unilateral Care Model
- Cost of precaution, wx
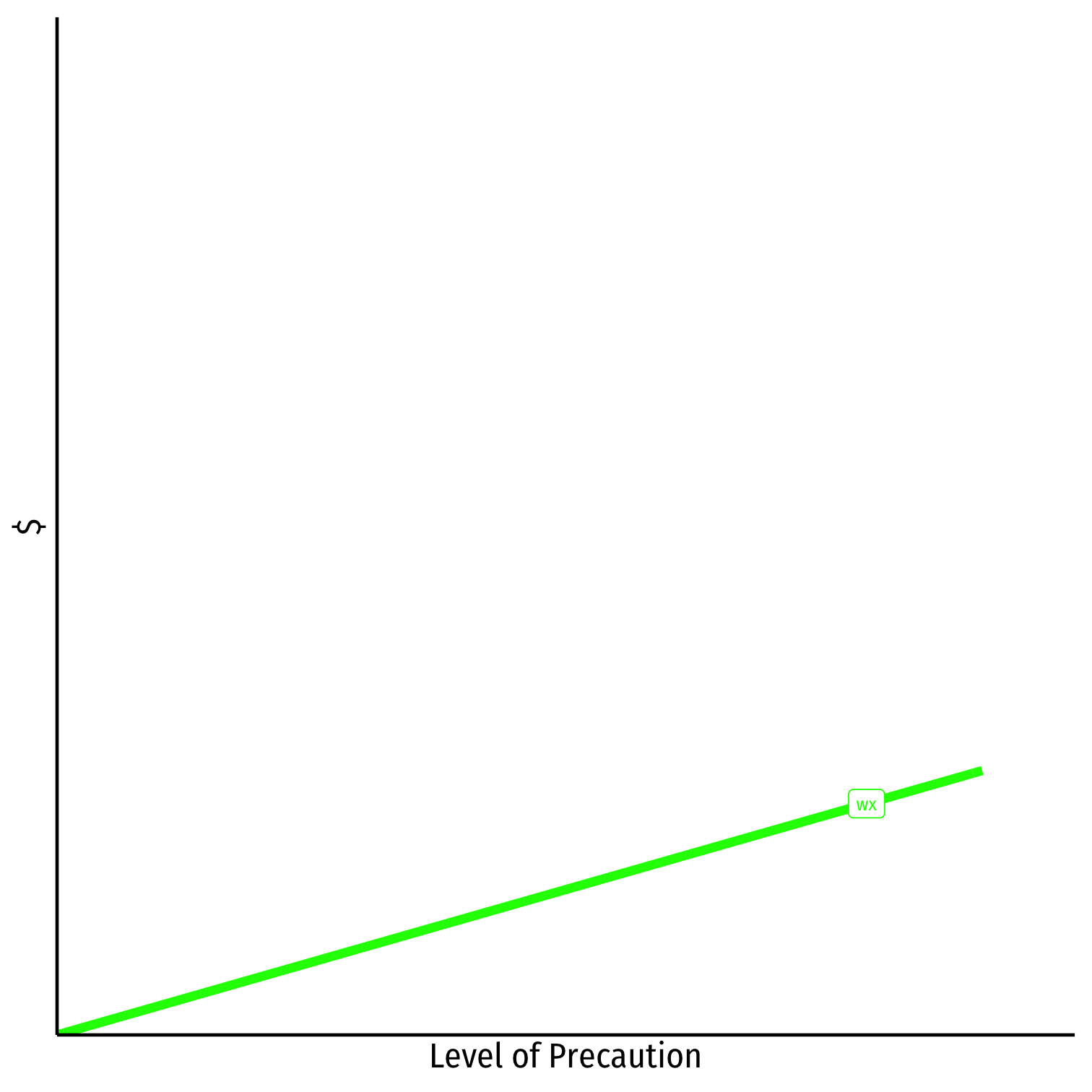
A Unilateral Care Model
Cost of precaution, wx
Cost of accidents, p(x)A
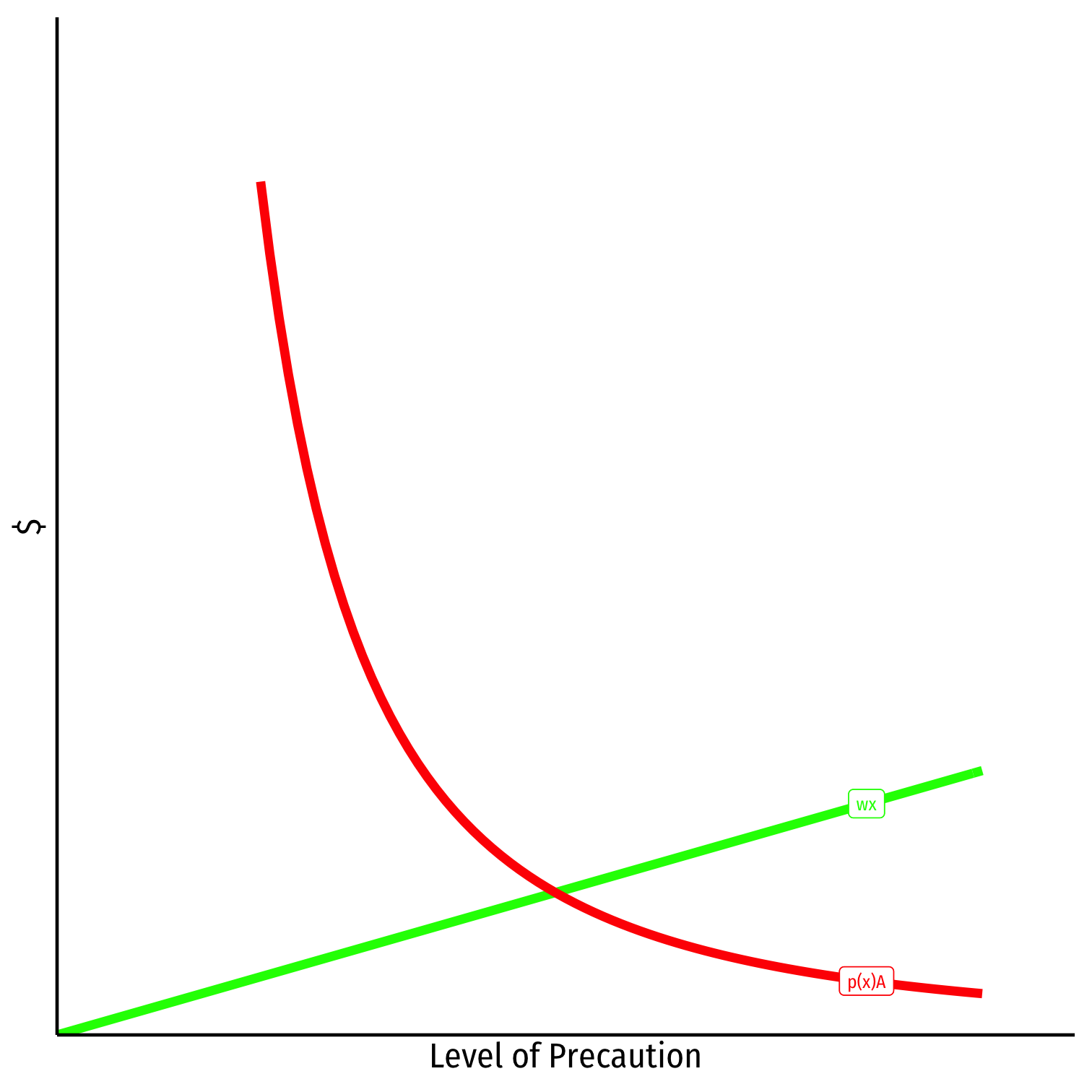
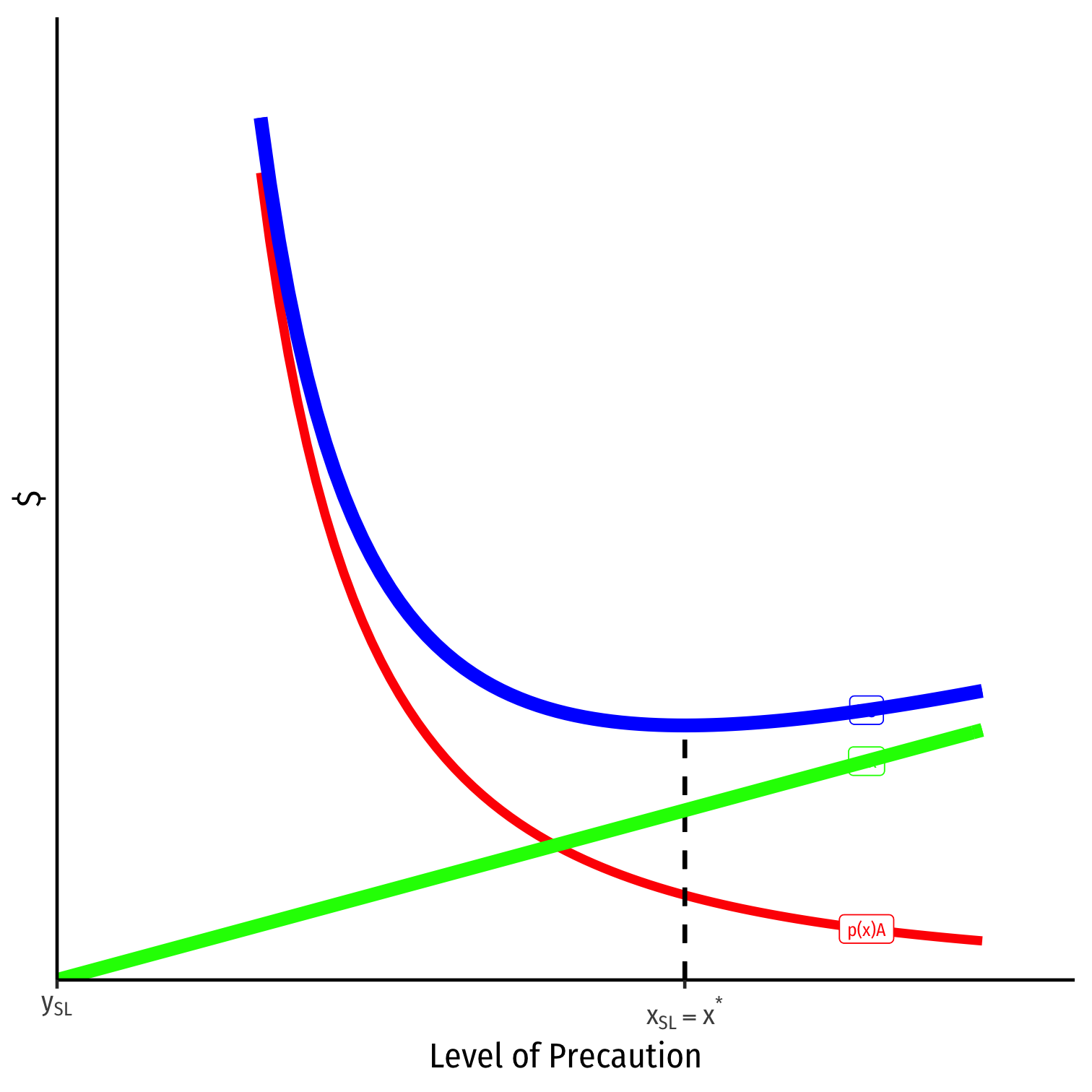
A Unilateral Care Model
Cost of precaution, wx
Cost of accidents, p(x)A
Total Social Cost p(x)A+wx
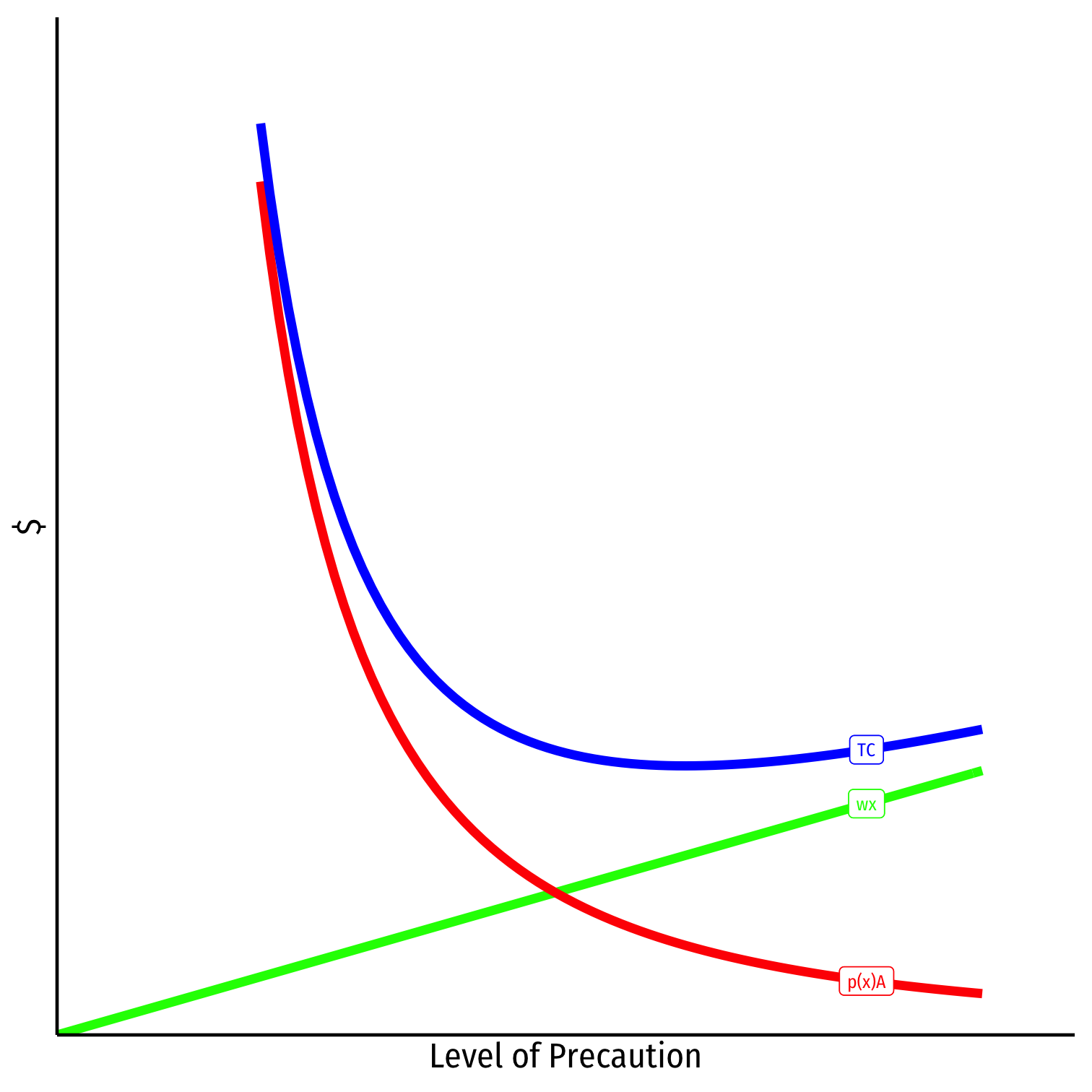
A Unilateral Care Model
Cost of precaution, wx
Cost of accidents, p(x)A
Total Social Cost p(x)A+wx
Efficient level of precaution:
minx colorbluep(x)A+wx
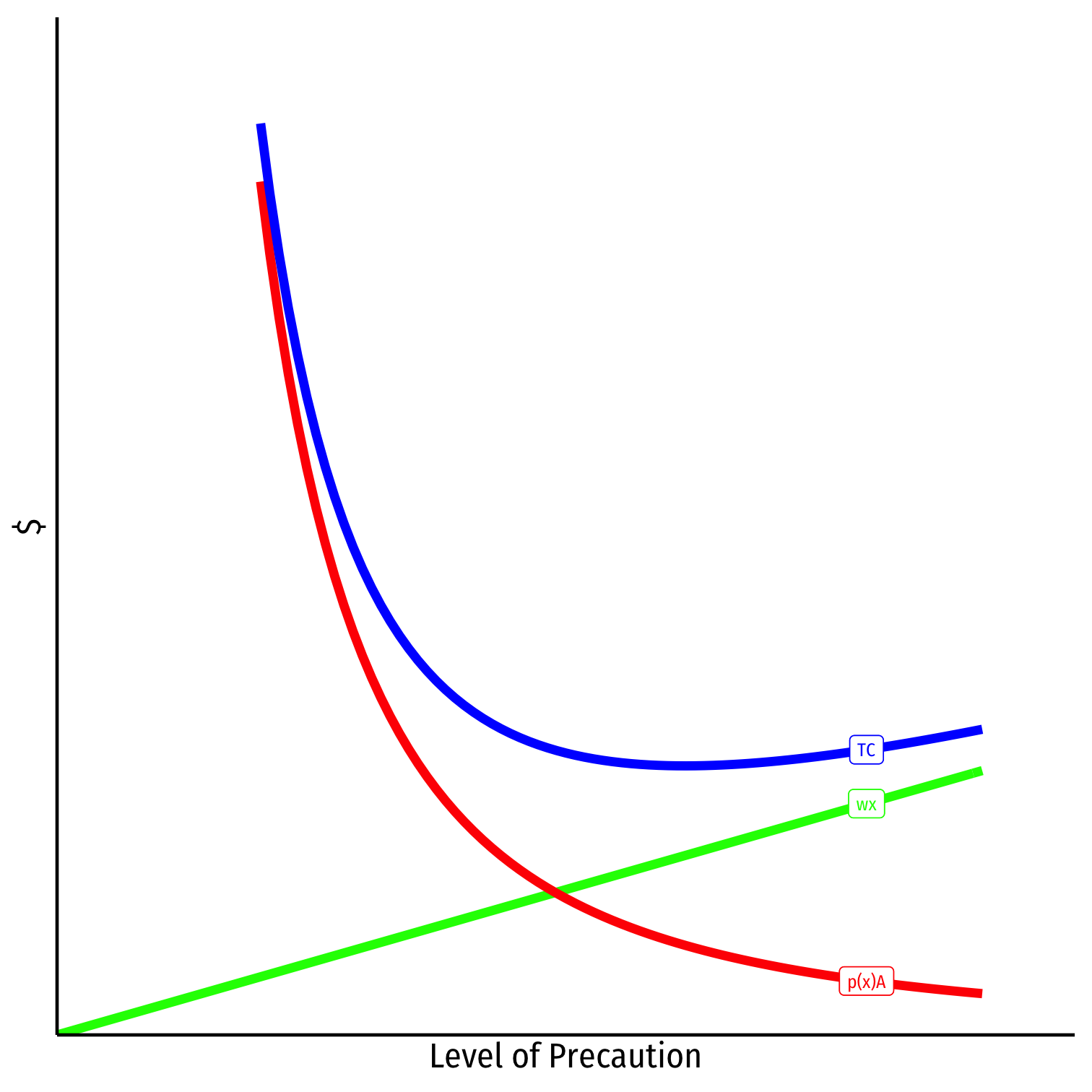
A Unilateral Care Model
Cost of precaution, wx
Cost of accidents, p(x)A
Total Social Cost p(x)A+wx
Efficient level of precaution:
minxp(x)A+wx
- Optimum x⋆:
w=−p′(x)AMSC of precaution=MSB of precaution
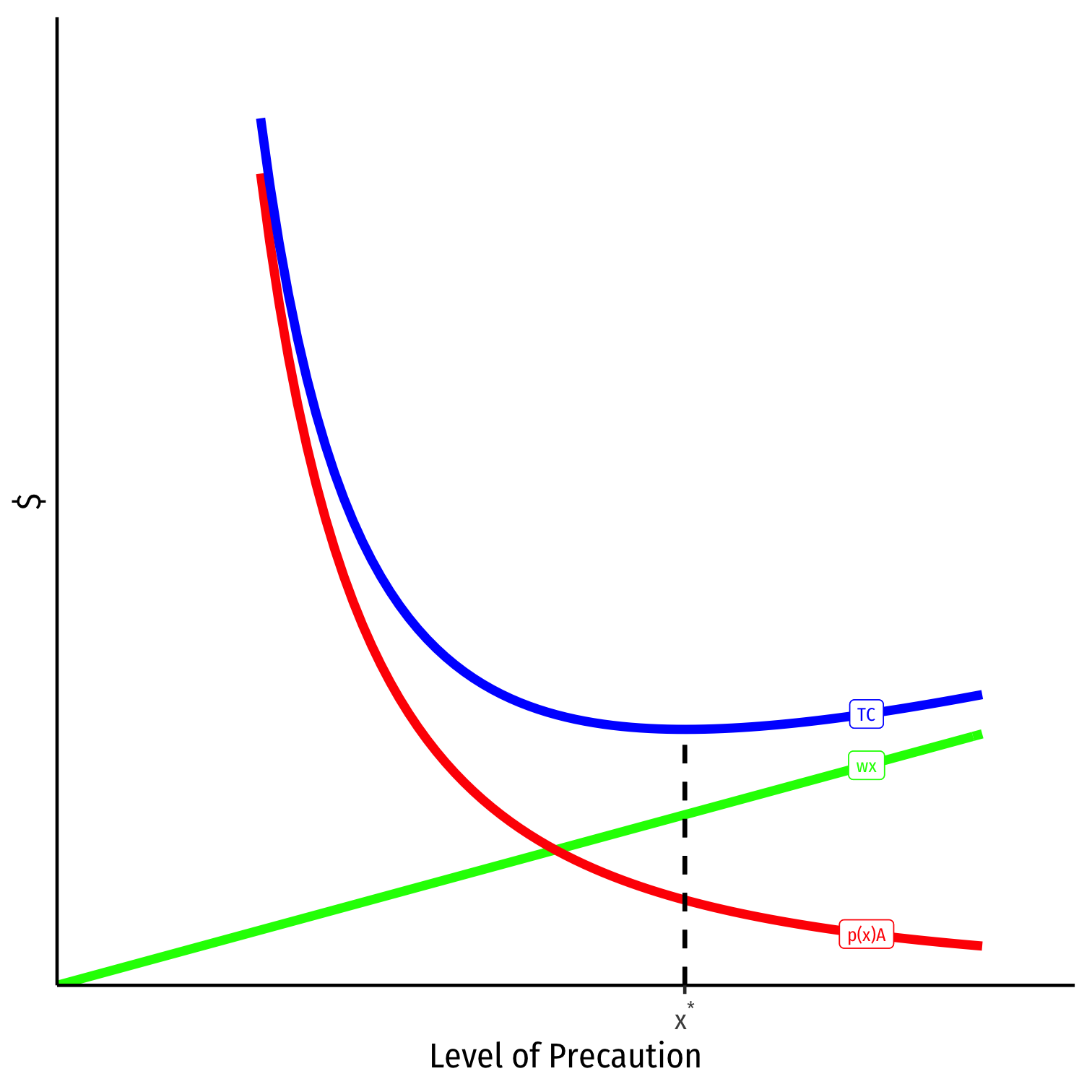
A Unilateral Care Model
- The efficient level of precaution, x⋆ minimizes total social cost
- Balances the tradeoff between the benefit of reduced accident likelihood and the cost of increased precaution
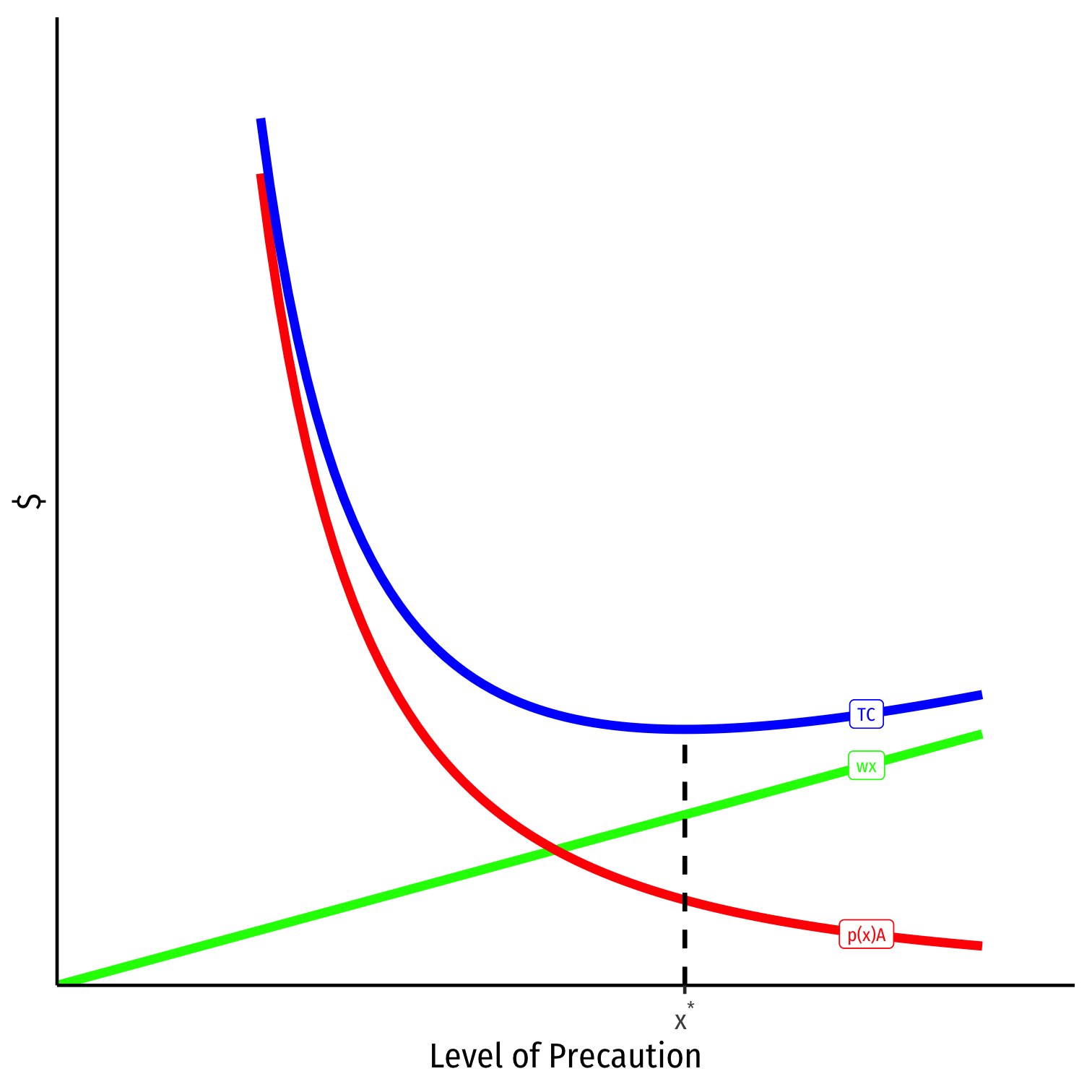
A Unilateral Care Model: Technical Note
We are thinking of bilateral precaution, just “one party at a time”; again:
- x represent level of precaution by injurer
- y represent level of precaution by victim
Really, the social problem between both parties: minx,yp(x,y)A−wx−wy
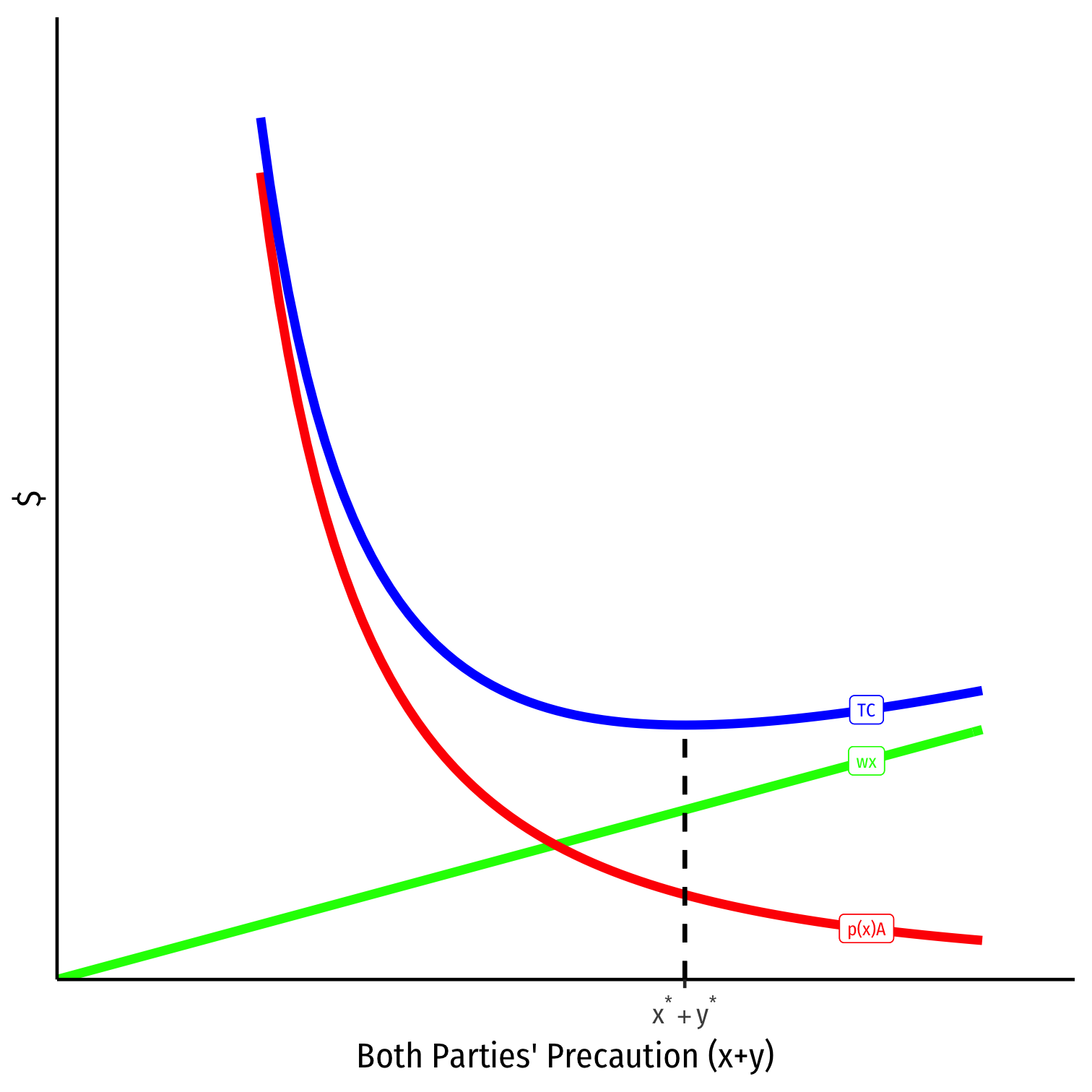
A Unilateral Care Model: Technical Note
- “Hold fixed” one party’s solution and consider the other, e.g.
minxp(x,y)A−wx−wy given y
- Results will generally be efficient given what the other party is doing
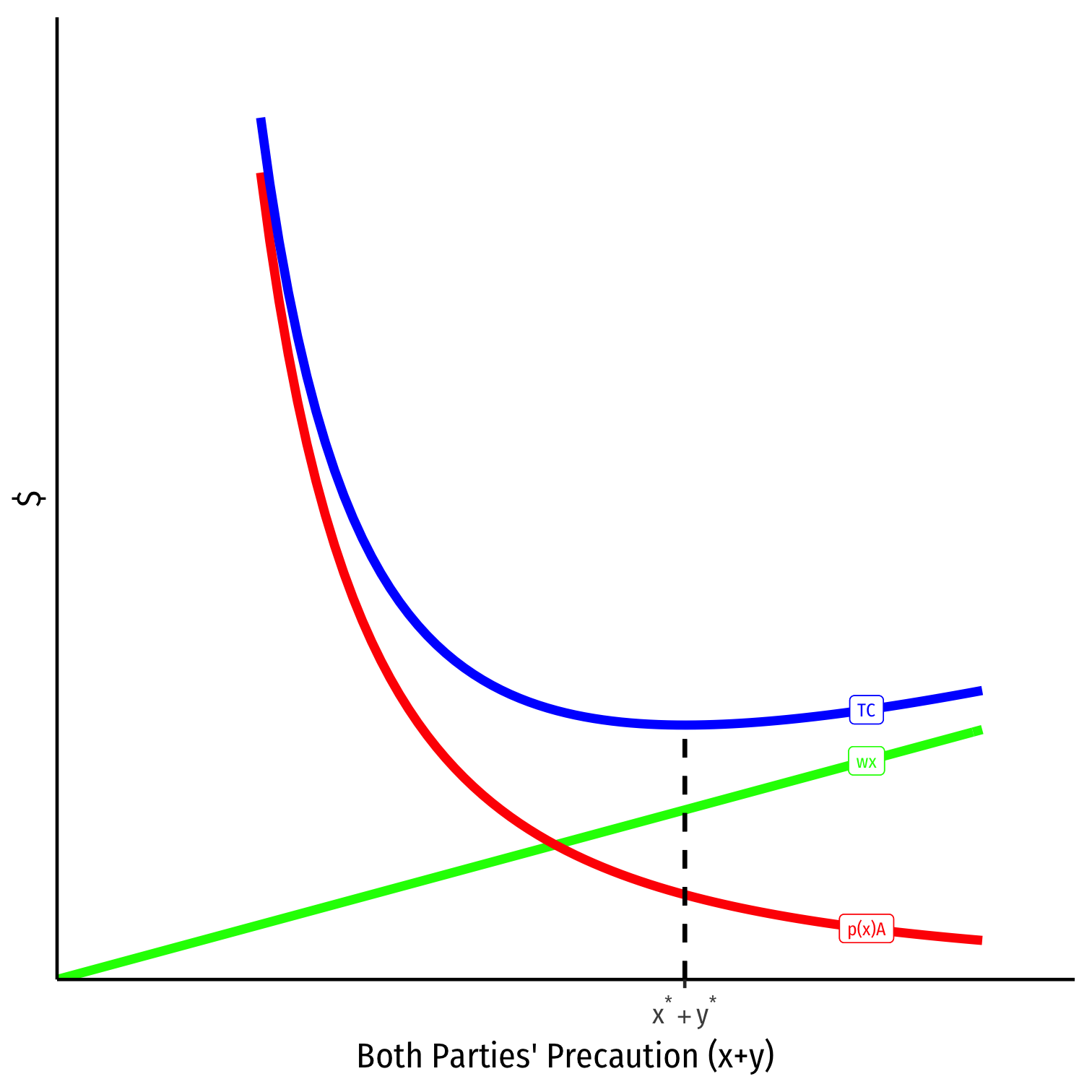
Effect of Liability Rules on Precaution
We know the efficient level of precaution is x⋆, which minimizes total social cost
Now let’s consider the effect of different liability rules have on the chosen amount of precaution

No Liability
No Liability
Imagine a world of no liability (NL)
Injurer pays nothing for accidents
- Bears the cost of his precaution
- But no benefit (of avoided damages)
- Has no incentive to take any precaution
Victim bears cost of any accidents, plus cost of her precaution taken
- Victim precaution imposes no externality on Injurer
- Victim will invest in efficient amount of precaution y⋆

No Liability
- Injurer's private costs: wx
minxwx⟹xNL=0
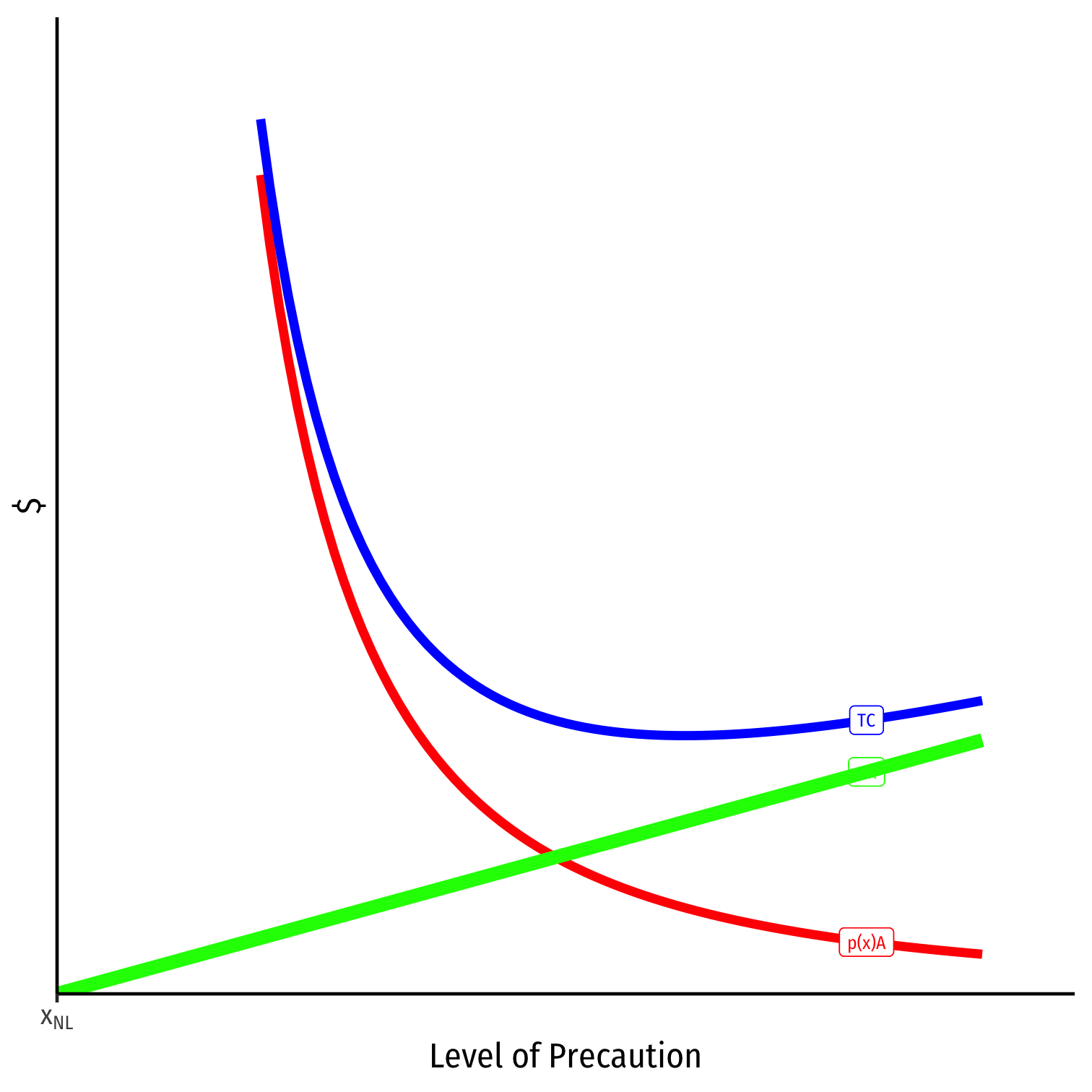
No Liability
Injurer's private costs: wx minxwx⟹xNL=0
Victim's private costs: p(y)A+wy minyp(y)A+wy⟹yNL=y⋆
- chooses efficient precaution
Rule of no liability leads to:
- efficient precaution by Victims
- no precaution by Injurers
Comparing Incentives Under Different Liability Rules
| Rule | Injurer Precaution | Victim Precaution |
|---|---|---|
| No liability | Zero | Efficient |
Determining Accidents
Precaution isn't the only thing that affects the number of accidents
- Precautions are extra actions that make our activity less dangerous
Also the amount of activities we do affects the number of accidents
- I decide how often to drive
- You decide how often to bike
Liability rules also create incentives for activity levels

Determining Accidents: No Liability
With no liability, I am not liable if I hit you
- I don't consider cost of accident when I decide how fast to drive
- nor when I decide how much to drive
- So I drive too recklessly and too often
My driving imposes a negative externality on others
- With no liability, Injurer's activity level is inefficiently high

Determining Accidents: No Liability
- With no liability, you bear the full cost of an accident
- More activity by victim (bicycling) leads to more accidents
- You weigh cost of accidents when deciding how carefully to ride, and how much to ride
- Your private cost equals the social cost
- You take the efficient level of precaution, and efficient level of activity
Comparing Incentives Under Different Liability Rules
| Rule | Injurer Precaution | Victim Precaution | Injurer Activity | Victim Activity |
|---|---|---|---|---|
| No liability | Zero | Efficient | Too High | Efficient |
Strict Liability
Strict Liability
Imagine a world of strict liability (SL) with perfect compensation
- D=A damages equal to the cost of the accident
Injurer pays for any accidents he causes
- Bears the full cost of accidents plus his precautions taken
- Receives benefit (of avoided damages)
- Internalizes externality his actions cause, chooses the efficient level of precaution
Victim is fully insured
- Has no incentive to invest in any precaution

Strict Liability
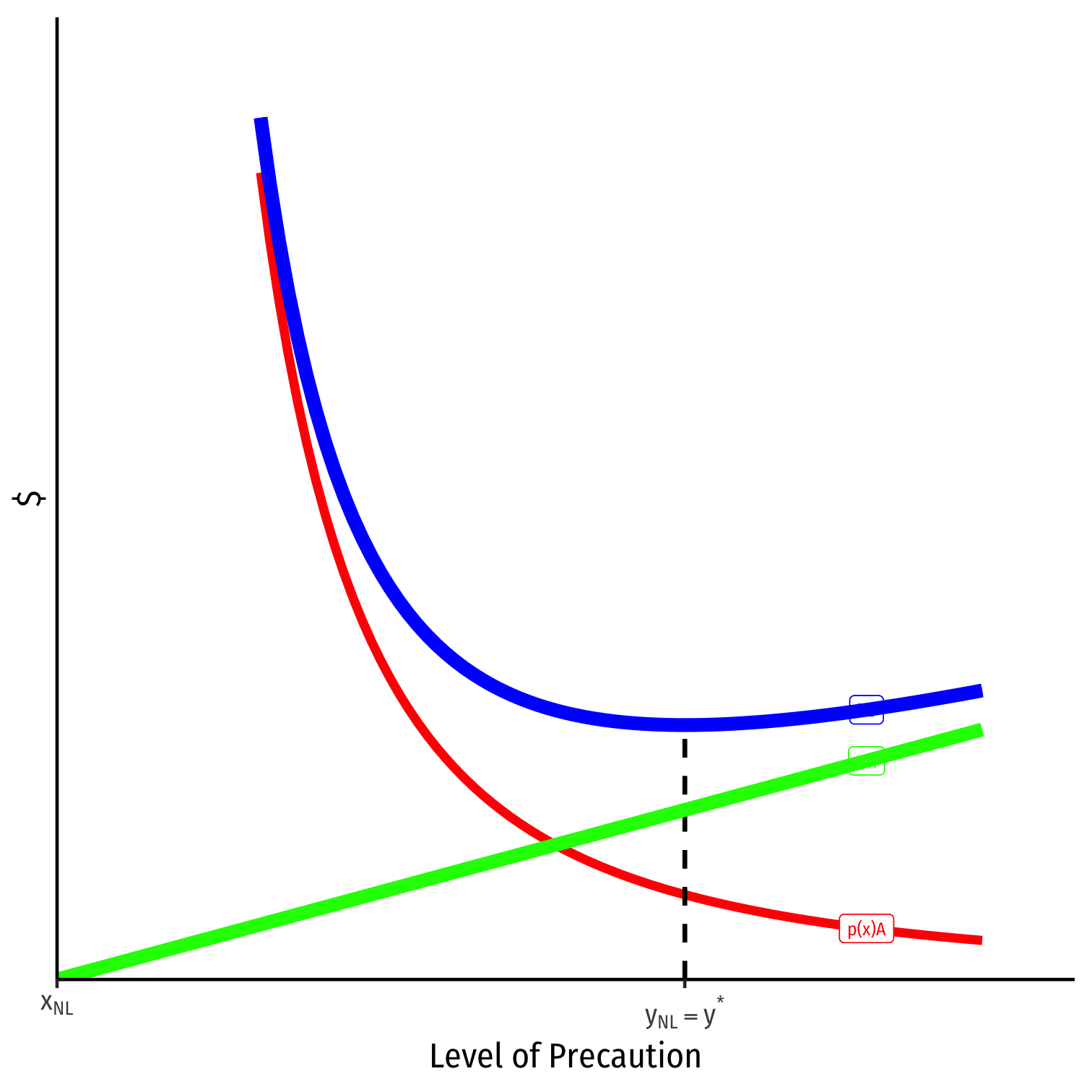
- Injurer's private costs: p(x)A+wx
minxp(x)A+wx⟹xSL=x⋆
- chooses efficient precaution
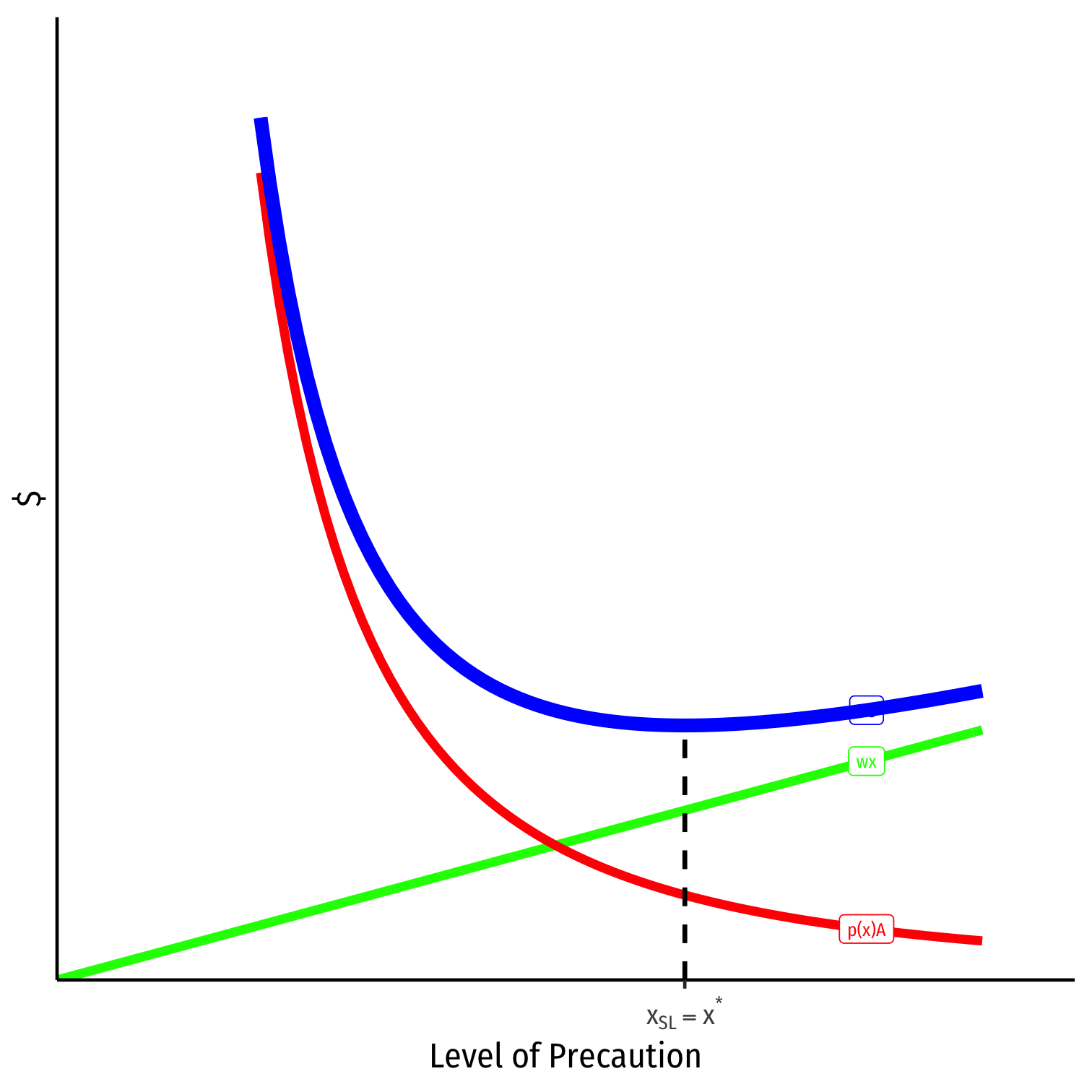
Strict Liability
Injurer's private costs: p(x)A+wx minxp(x)A+wx⟹xSL=x⋆
- chooses efficient precaution
Victim's private costs: wy minywy⟹ySL=0
Rule of strict liability leads to:
- efficient precaution by Injurers
- no precaution by Victims
Comparing Incentives Under Different Liability Rules
| Rule | Injurer Precaution | Victim Precaution |
|---|---|---|
| No liability | Zero | Efficient |
| Strict liability | Efficient | Zero |
Strict Liability: Activity Levels
Under strict liability, injurer internalizes cost of accidents
- Weighs benefit from driving against cost of accidents
- Takes efficient activity level
Under strict liability, victim does not bear cost of accidents
- Ignores cost of accidents when deciding how much to bicycle
- Takes inefficiently high activity level
Strict liability leads to efficient level of injurer activity, inefficiently high level of victim activity

Comparing Incentives Under Different Liability Rules
| Rule | Injurer Precaution | Victim Precaution | Injurer Activity | Victim Activity |
|---|---|---|---|---|
| No liability | Zero | Efficient | Too High | Efficient |
| Strict liability | Efficient | Zero | Efficient | Too High |
Comparing Incentives Under Different Liability Rules
So for both precaution & activity level:
No liability leads to inefficient behavior by injurer, efficient behavior by victim
Strict liability leads to efficient behavior by injurer, inefficient behavior by victim
Like the paradox of compensation from contract law!
- One rule sets multiple incentives...we can't get them all right
- ...or can we? Tort law has this One Weird TrickTM

Negligence
Negligence
Negligence rule: Injurer is only liable if he breached his duty of due care
- Put alternatively, liable only if accident is “his fault”
Within our model:
- Legal standard of care xl
- Injurer owes damages if x<xl
- If x<xl→D=A
- If x≥xl→D=0

Negligence
- Private cost to injurer is:
Negligence
- Private cost to injurer is:
{p(x)A+wxif x<xl
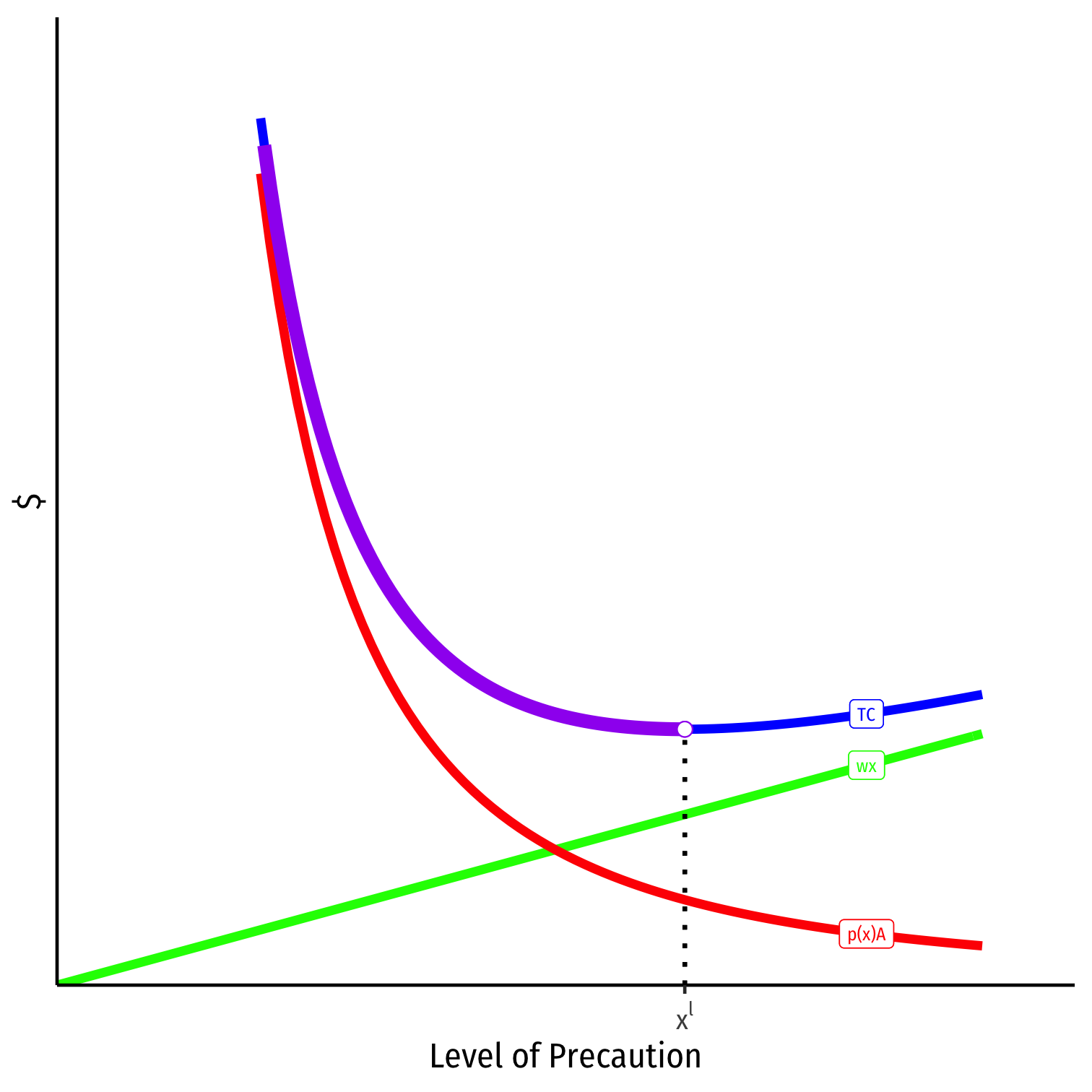
Negligence
- Private cost to injurer is:
{p(x)A+wxif x<xlwxif x≥xl
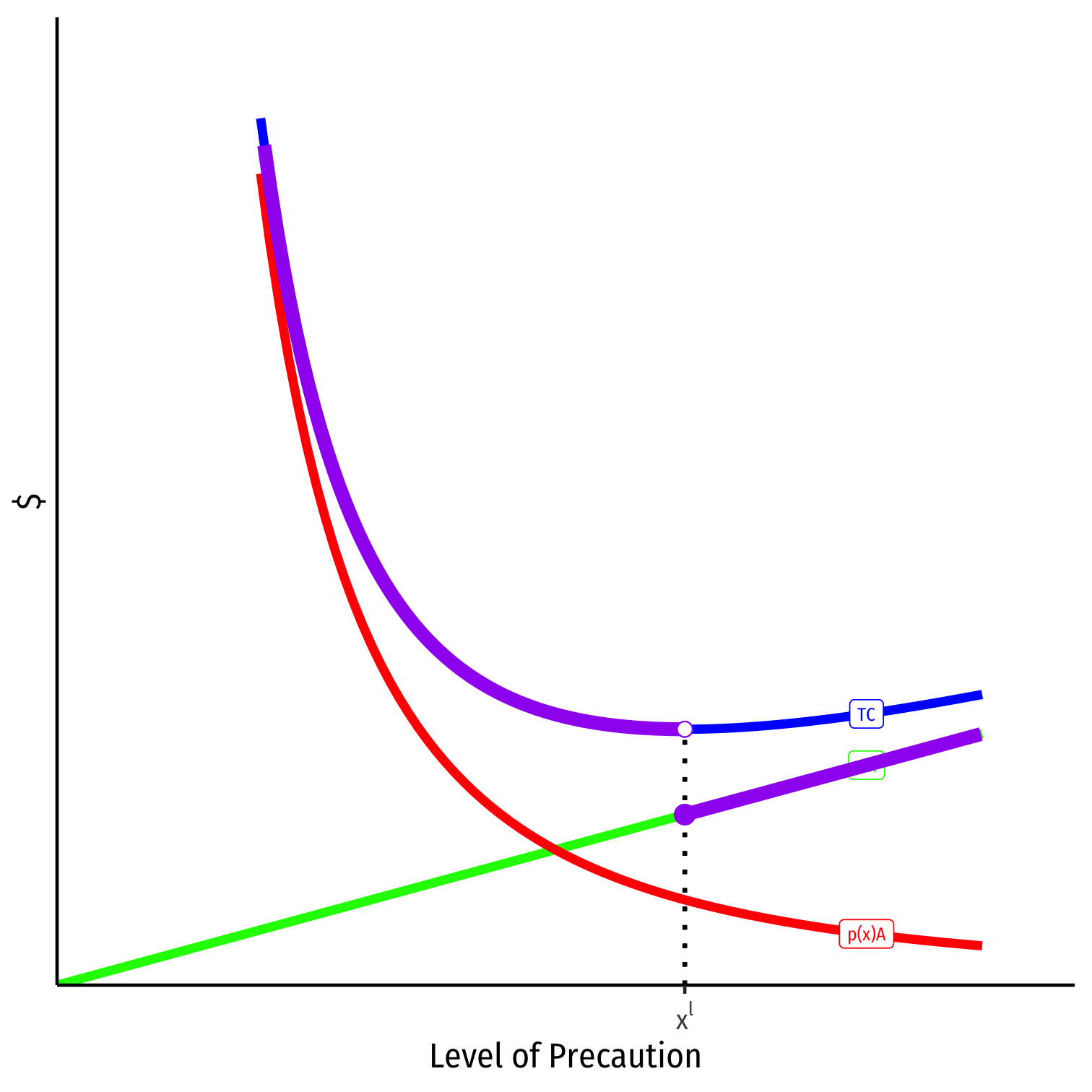
Negligence
Private cost to injurer is: {p(x)A+wxif x<xlwxif x≥xl
If standard of care xl is set to x⋆, injurer minimizes private cost by taking efficient caution
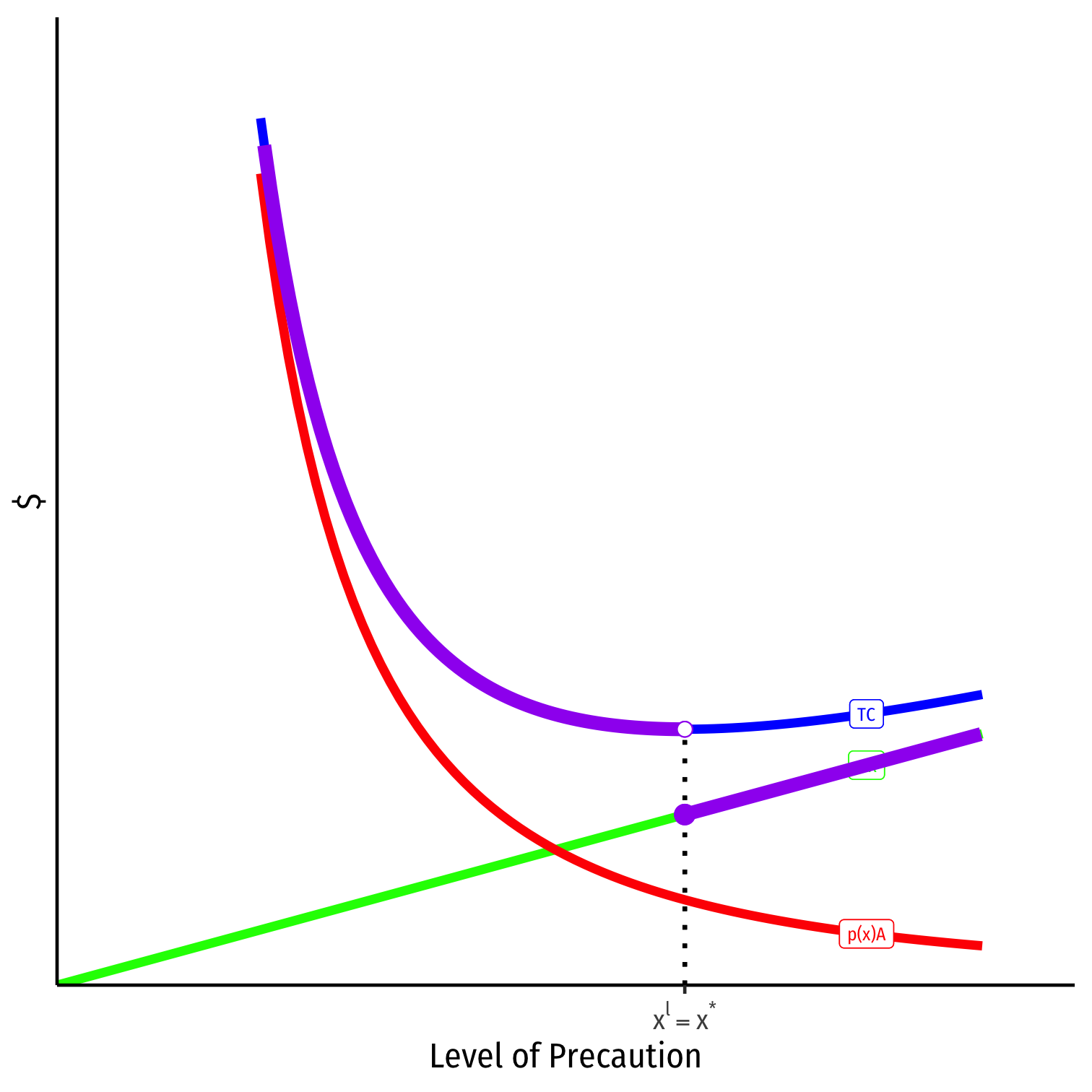
Negligence: Injurer Precaution
What about victim's incentives?
- We saw injurer will exercise due care and not be liable!
- Victim now bears cost of any accidents! (residual risk)
Private cost to victim is: p(y)A+wy
- Victim chooses y⋆, efficient precaution too!
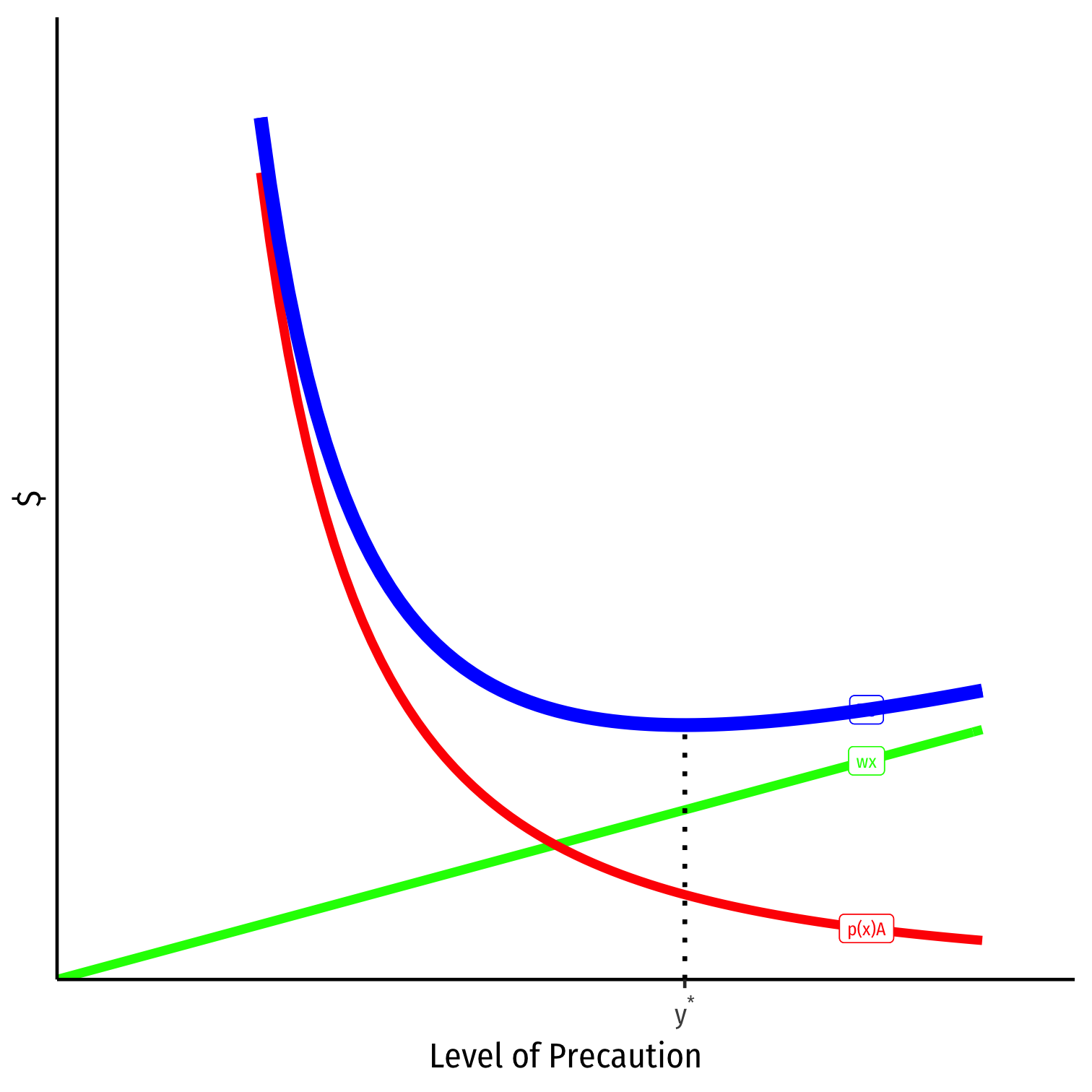
Comparing Incentives Under Different Liability Rules
| Rule | Injurer Precaution | Victim Precaution | Injurer Activity | Victim Activity |
|---|---|---|---|---|
| No liability | Zero | Efficient | Too High | Efficient |
| Strict liability | Efficient | Zero | Efficient | Too High |
| Negligence† | Efficient | Efficient |
† Assuming standard of care is set at the efficient level (xl=x∗)
A Family of Negligence Rules
Other Negligence Rules
The rule we just considered is “simple” negligence
- Only consider injurer's actions in determining liability
But in deciding whether injurer should be liable, we could also consider whether the victim was negligent

Contributory Negligence: Butterfield v. Forrester
Butterfield v. Forrester, 11 East. 60, 103 Eng. Rep. 926 (K.B. 1809)
Forrester (Defendent) placed a pole in road next to his house while making repairs
Butterfield (Plaintiff) was riding at high speed at night, hit the pole, fell off his horse, sued for damages
Witness said that if Forrester had not been riding fast, would have seen the pole
Jury ruled Plaintiff should not be able to collect damages from Plaintiff due to their own contributory negligence

“One person being in fault will not dispense with another’s using ordinary care for himself.”
Injurer & Victim Negligence
Let’s compare the whole family of negligence rules
Injurer is negligent/at fault when they fail to take due care, x<x∗†
Victim is negligent/at fault when they fail to take due care, y<y∗†
Now let’s consider who is liable for the accident under various negligence rules
† Assuming standards of care are set at the efficient levels xl=x⋆ and yl=y⋆
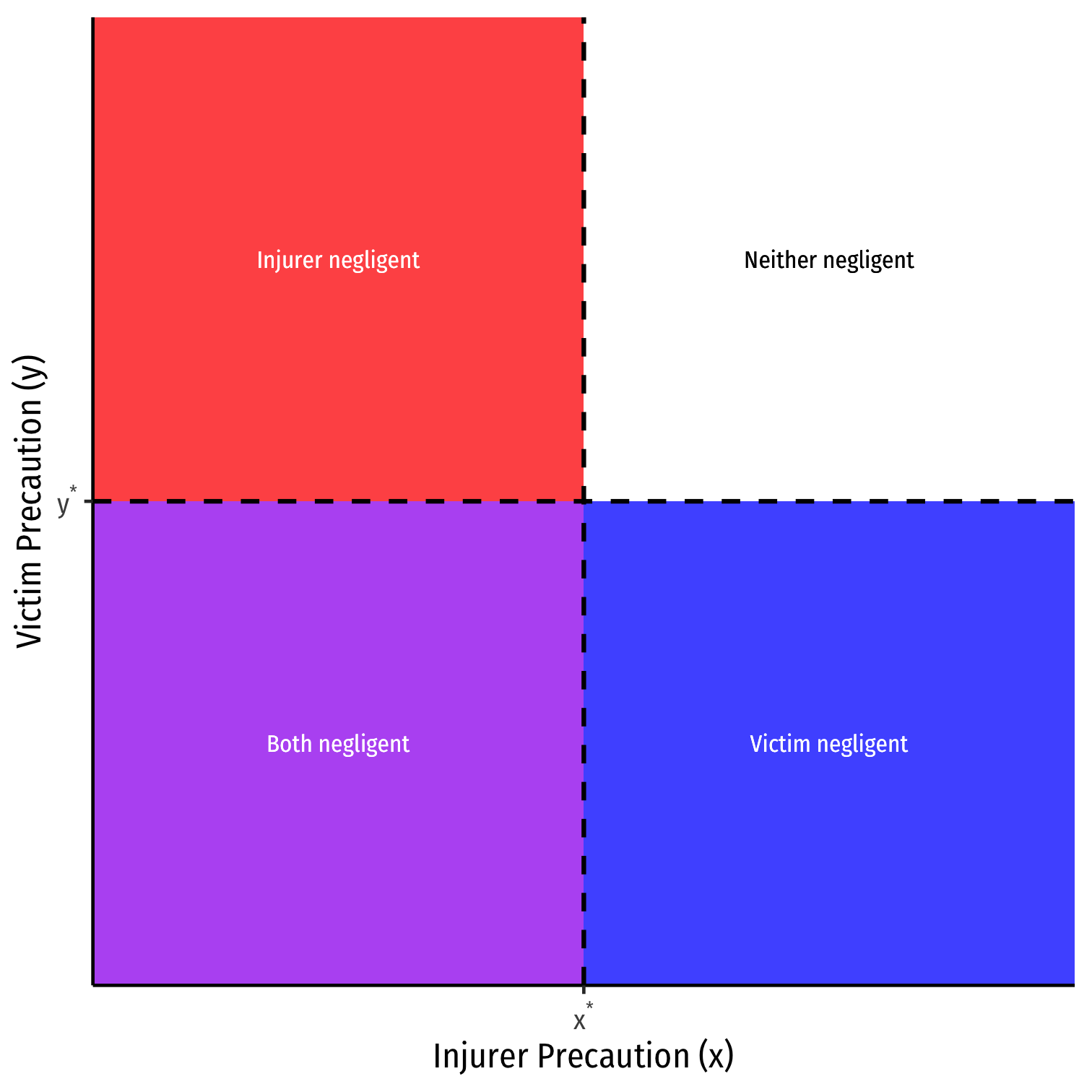
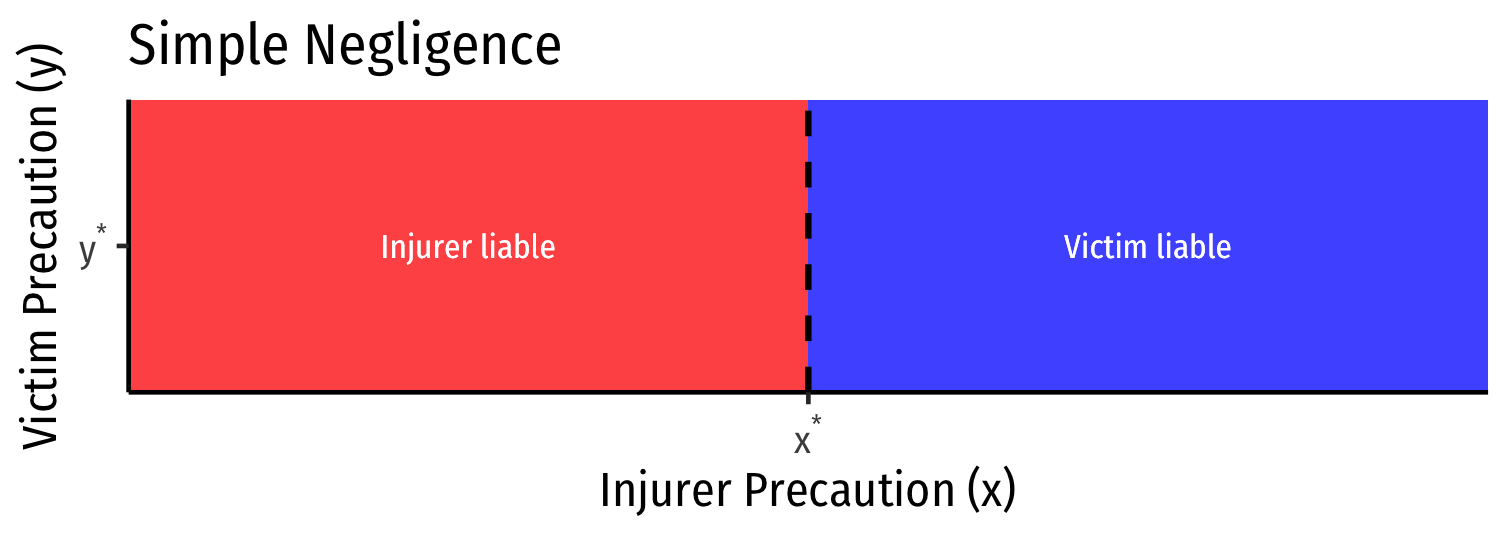
Simple Negligence
Simple negligence:
Injurer is liable if they do not take due care x<x∗
Injurer is not liable if they do take due care x≥x∗
- Victim cannot collect damages for any accident
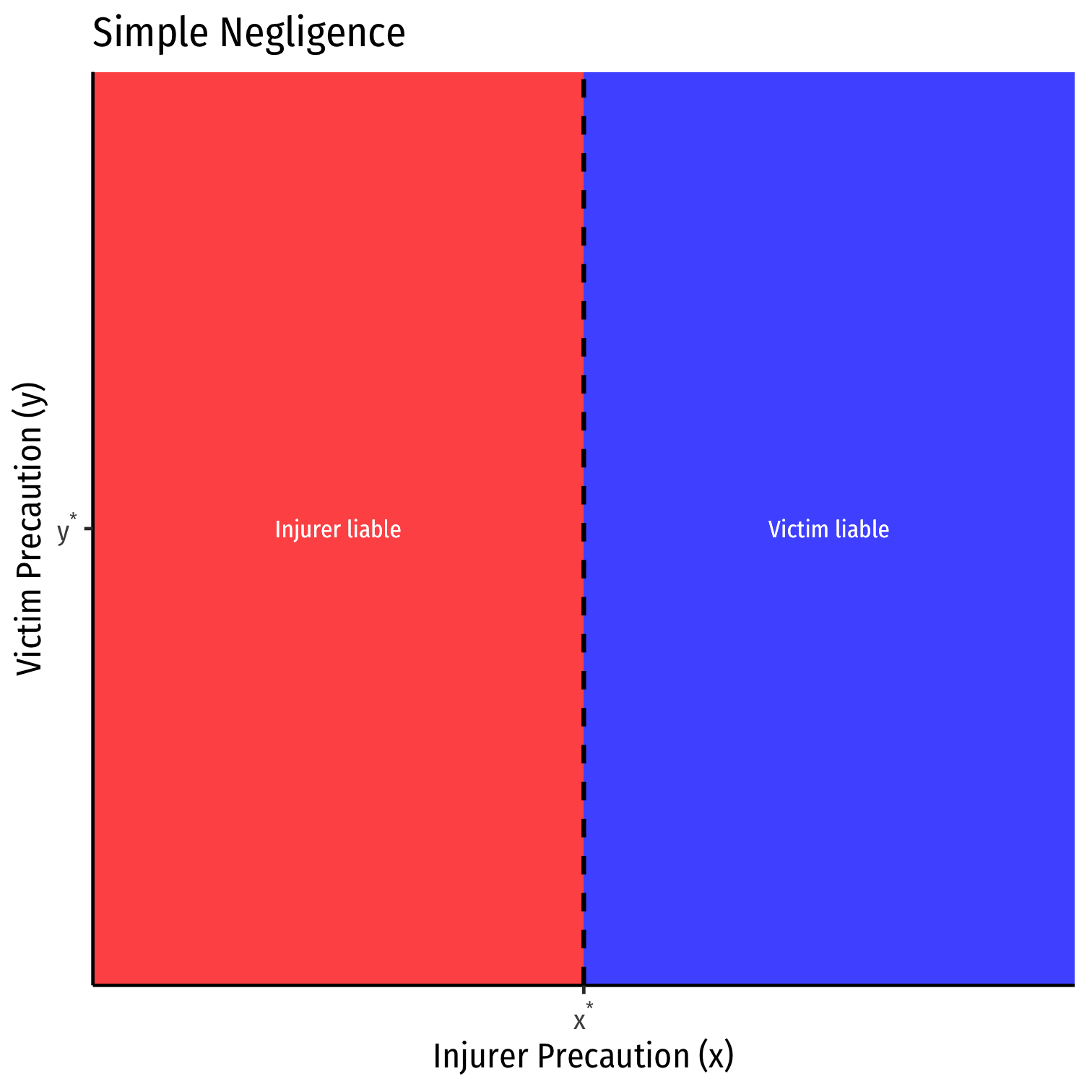
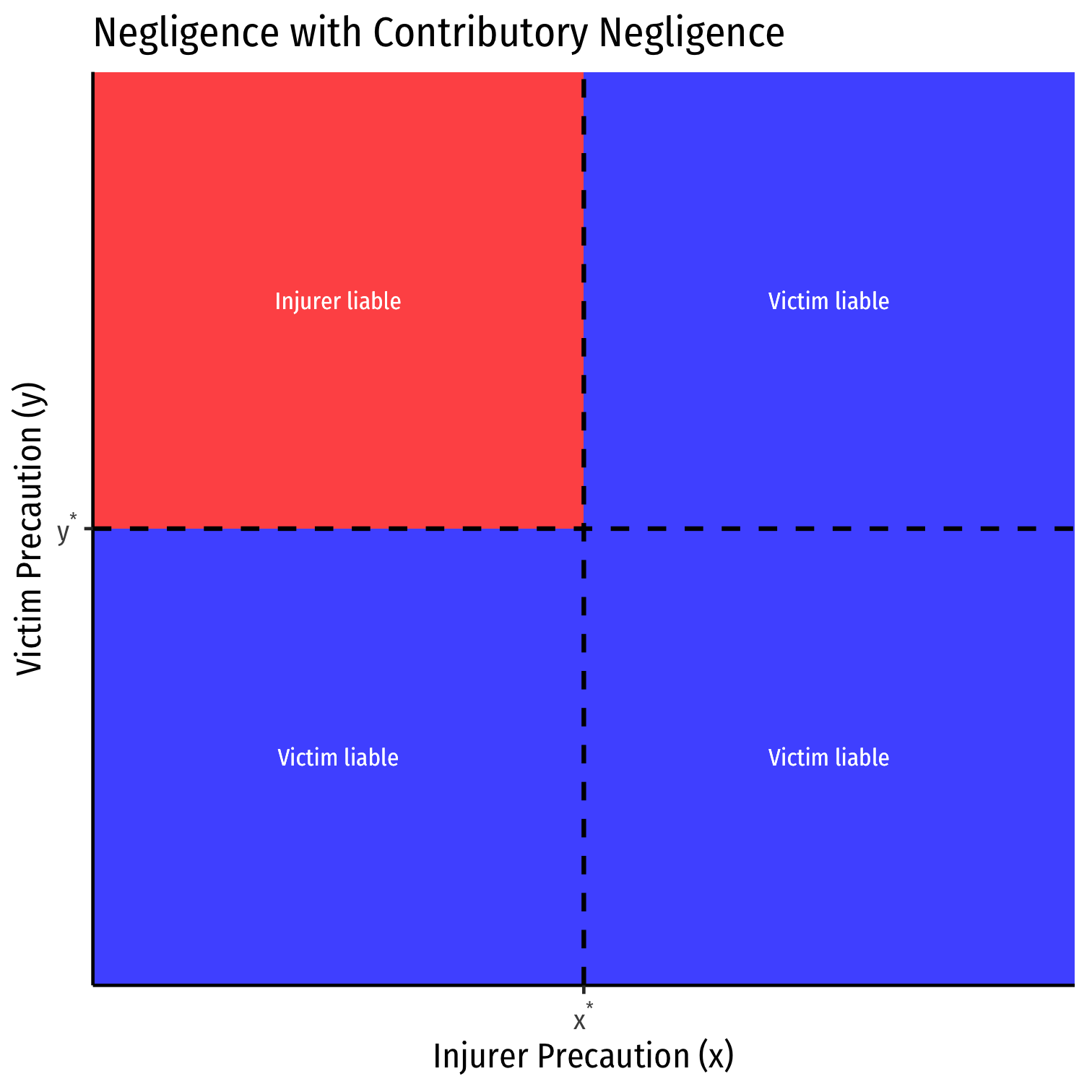
Negligence With a Defense of Contributory Negligence
Negligence with a defense of Contributory Negligence:
Injurer is liable if they do not take due care x<x∗
Injurer is not liable if Victim does not take due care y<y∗
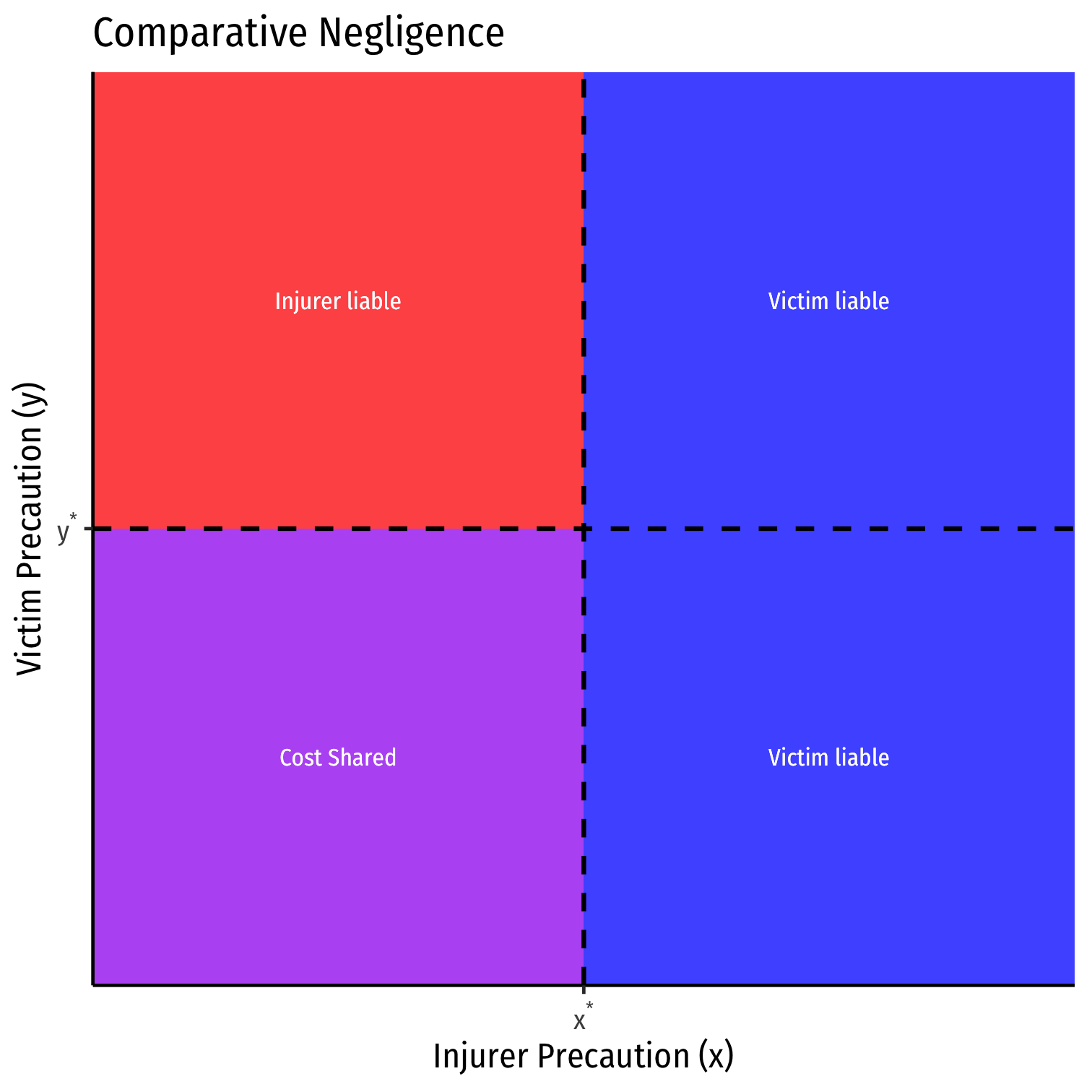
Comparative Negligence
- Comparative Negligence: if both parties are negligent, they share the cost of the accident (possibly proportionately)
- e.g. if accident cause was 70% injurer’s fault, 30% victim’s fault, injurer pays for 70% of damages
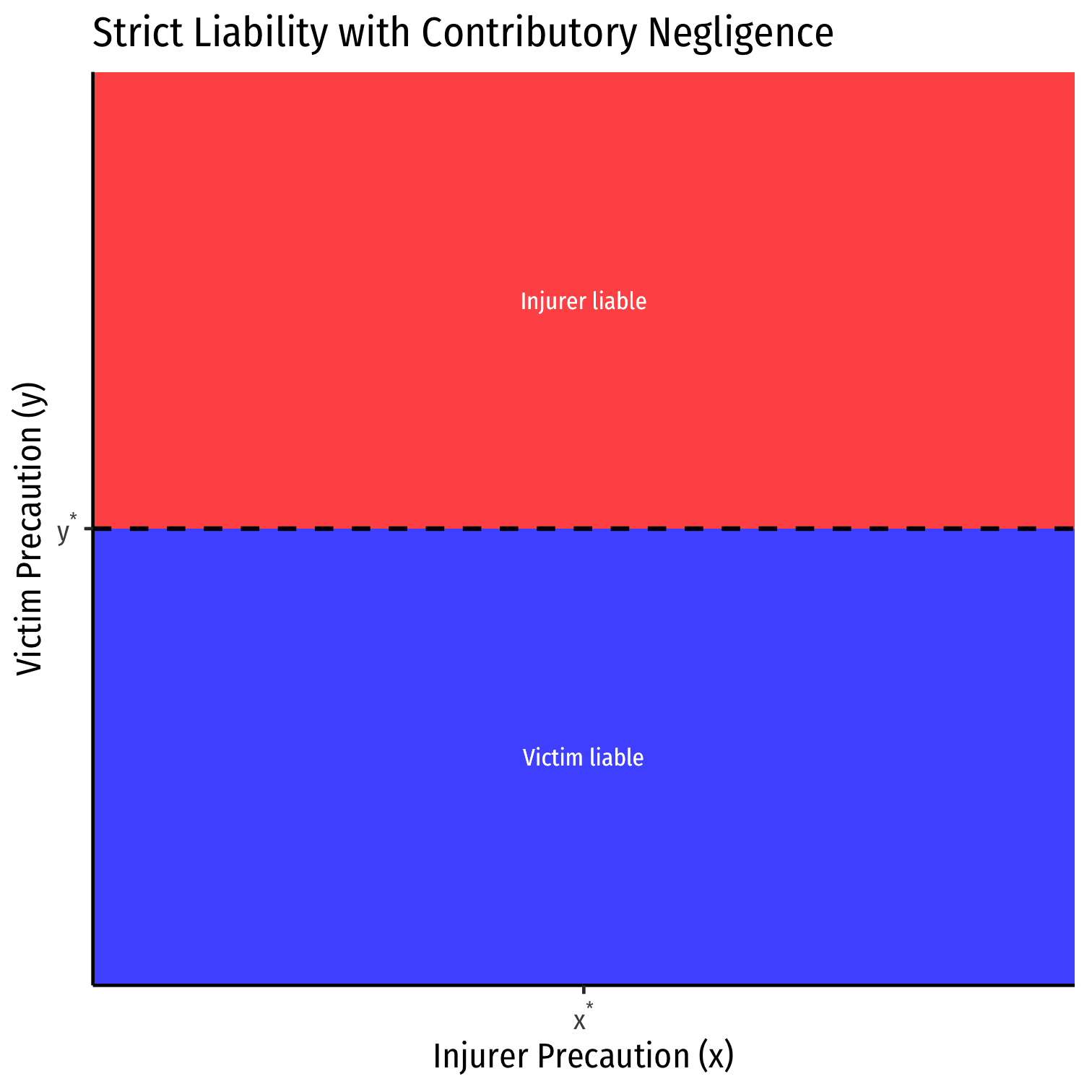
Strict liability with Contributory Negligence
Strict liability with defense of Contributory Negligence:
Injurer is liable (regardless of their level of precaution x) unless Victim does not take due care y<y∗
Family of Negligence Rules
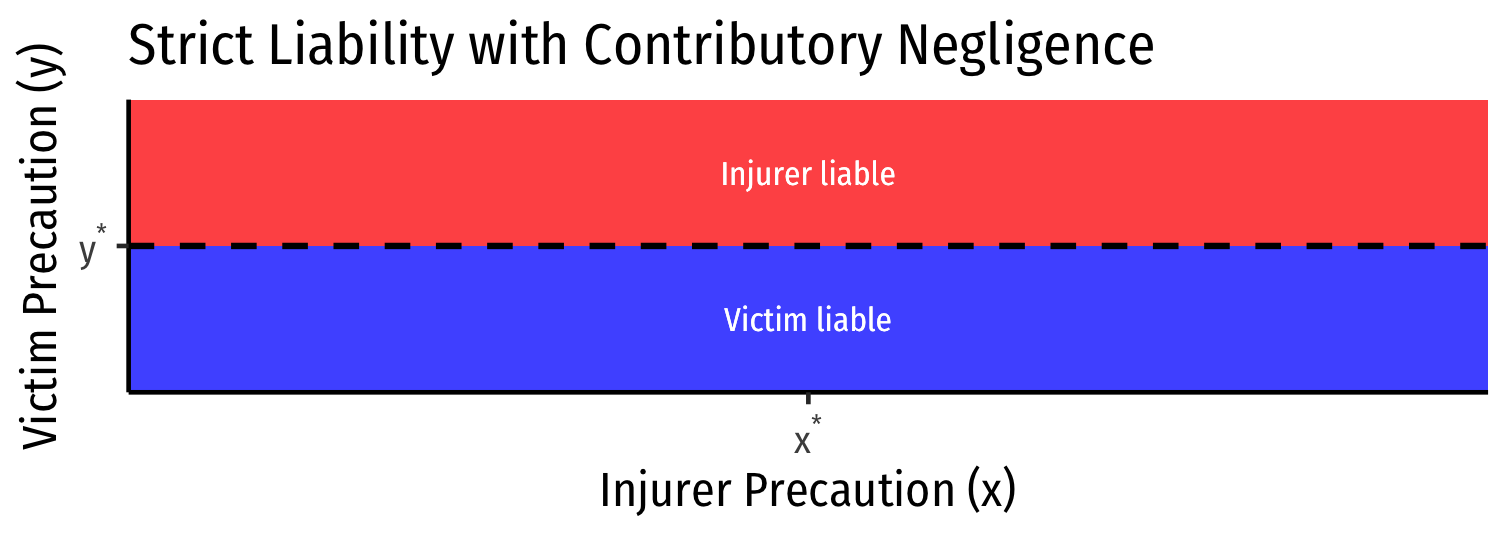
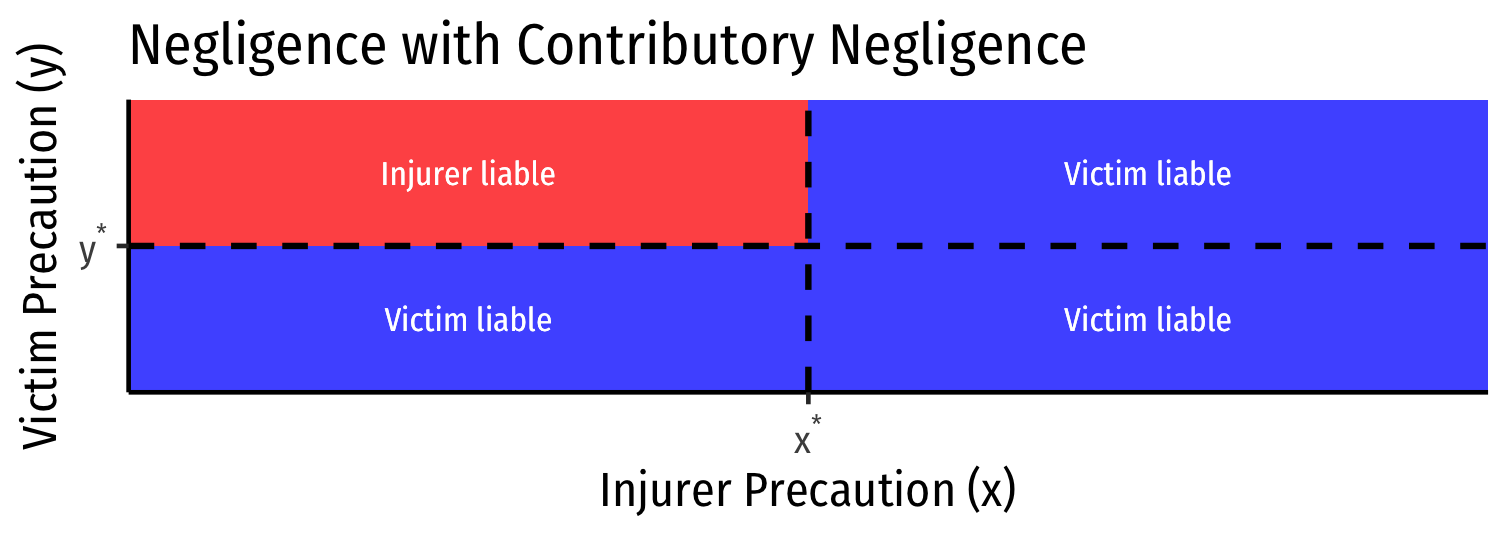
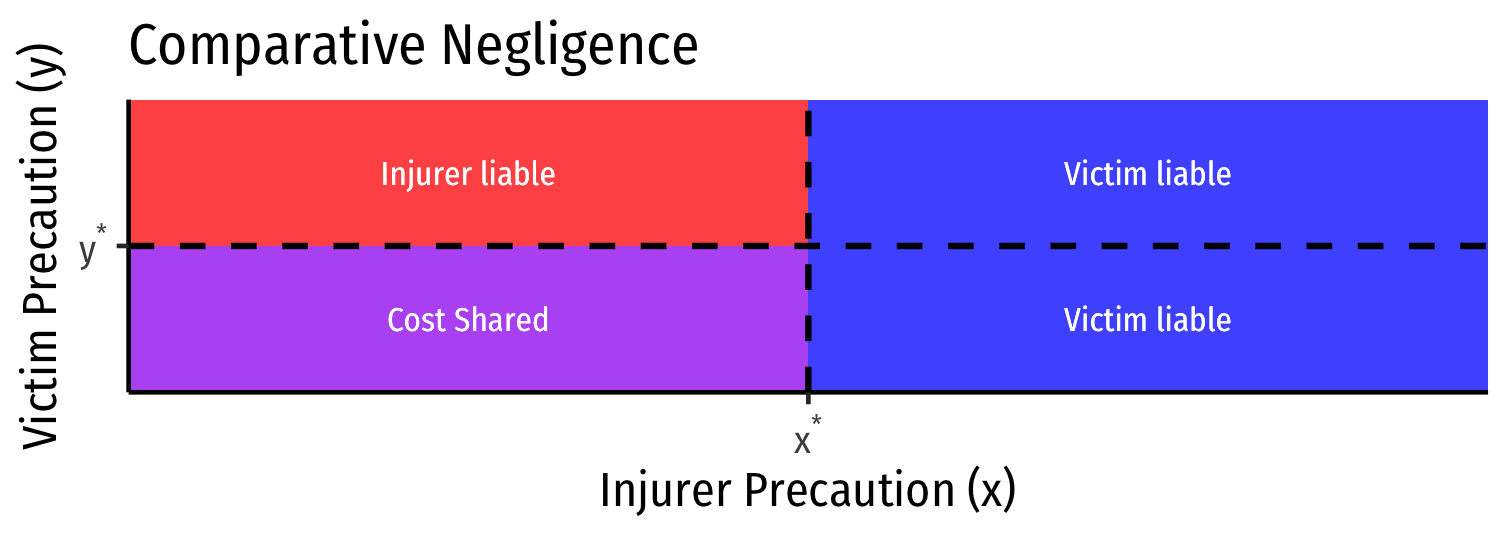
Family of Negligence Rules




These rules differ only in distribution of income
Any of these rules (with efficient standard of care) incentivize efficient precaution by both parties! (x⋆,y⋆)
Comparing Negligence Rules, A Discrete Example of Bilateral Caution
Discrete Example of Bilateral Precaution
Let's compare with a discrete example
Each party Injurer and Victim can either take precaution or not
- Precaution costs each party $20
- Each accident costs $1,000 in harm
Chance of accident is:
- 10% if nobody takes precaution
- 6% if one party takes precaution
- 2% if both parties take precaution
Note: precaution is efficient for each party: costs $20; reduces expected damage by 0.04($1,000) = $40

A: $1,000
w: $20 (each party)
p: 10% (neither), 6% (one careful), 2% (both)
Discrete Example of Bilateral Precaution
Consider rule of negligence with defense of contributory negligence
Injurer is liable if he failed to take precaution...unless blue victim failed too

A: $1,000
w: $20 (each party)
p: 10% (neither), 6% (one careful), 2% (both)
Discrete Example of Bilateral Precaution
Consider rule of negligence with defense of contributory negligence
Injurer is liable if he failed to take precaution...unless blue victim failed too
Notice Victim's dominant strategy is Precaution
- If Injurer not taking precaution, victim wants to avoid liability
- If Injurer takes precaution, victim bears residual risk, wants to minimize accidents

A: $1,000
w: $20 (each party)
p: 10% (neither), 6% (one careful), 2% (both)
Discrete Example of Bilateral Precaution
Consider rule of negligence with defense of contributory negligence
Injurer is liable if he failed to take precaution...unless blue victim failed too
Notice Victim's dominant strategy is Precaution
- If Injurer not taking precaution, victim wants to avoid liability
- If Injurer takes precaution, victim bears residual risk, wants to minimize accidents
For Injurer, best response to Victim's precaution is precaution
Nash Eq.: (Precaution, precaution), efficient!

A: $1,000
w: $20 (each party)
p: 10% (neither), 6% (one careful), 2% (both)
Discrete Example of Bilateral Precaution
- Consider rule of comparative negligence, cost of accident divided proportionately

A: $1,000
w: $20 (each party)
p: 10% (neither), 6% (one careful), 2% (both)
Discrete Example of Bilateral Precaution
Consider rule of comparative negligence, cost of accident divided proportionately
Notice Victim's dominant strategy is Precaution

A: $1,000
w: $20 (each party)
p: 10% (neither), 6% (one careful), 2% (both)
Discrete Example of Bilateral Precaution
Consider rule of comparative negligence, cost of accident divided proportionately
Notice Victim's dominant strategy is Precaution
For Injurer, best response to Victim's precaution is precaution
Nash Equilibrium: (Precaution, precaution) and is efficient!

A: $1,000
w: $20 (each party)
p: 10% (neither), 6% (one careful), 2% (both)
Discrete Example of Bilateral Precaution
Consider rule of strict liability with defense of contributory negligence
Injurer is liable regardless of his precaution ... unless blue victim was negligent

A: $1,000
w: $20 (each party)
p: 10% (neither), 6% (one careful), 2% (both)
Discrete Example of Bilateral Precaution
Consider rule of strict liability with defense of contributory negligence
Injurer is liable regardless of his precaution ... unless blue victim was negligent
Notice Victim's dominant strategy is Precaution

A: $1,000
w: $20 (each party)
p: 10% (neither), 6% (one careful), 2% (both)
Discrete Example of Bilateral Precaution
Consider rule of strict liability with defense of contributory negligence
Injurer is liable regardless of his precaution ... unless blue victim was negligent
Notice Victim's dominant strategy is Precaution
For Injurer, best response to Victim's precaution is precaution
Nash Equilibrium: (Precaution, precaution) and is efficient!

A: $1,000
w: $20 (each party)
p: 10% (neither), 6% (one careful), 2% (both)
Comparing Incentives Under Different Liability Rules
| Rule | Injurer Precaution | Victim Precaution | Injurer Activity | Victim Activity |
|---|---|---|---|---|
| No liability | Zero | Efficient | Too High | Efficient |
| Strict liability | Efficient | Zero | Efficient | Too High |
| (“Simple”) Negligence | Efficient | Efficient | ||
| Negligence w/Contributory Negligence | Efficient | Efficient | ||
| Comparative Negligence | Efficient | Efficient | ||
| Strict Liability w/Contributory Negligence | Efficient | Efficient |
Assuming all relevant standards of care are set at the efficient levels (xl=x∗)
Activity Levels under Negligence Rules
Simple negligence: injurer liable if he was negligent
Leads injurer to take efficient precaution, so injurer expects to not be liable for any accidents
So Injurer ignores cost of accidents when deciding on activity level
- Drives carefully, but still drives too much
Victim bears residual risk
- Bikes carefully, and bikes efficient amount

Comparing Incentives Under Different Liability Rules
| Rule | Injurer Precaution | Victim Precaution | Injurer Activity | Victim Activity |
|---|---|---|---|---|
| No liability | Zero | Efficient | Too High | Efficient |
| Strict liability | Efficient | Zero | Efficient | Too High |
| (“Simple”) Negligence | Efficient | Efficient | Too High | Efficient |
| Negligence w/Contributory Negligence | Efficient | Efficient | ||
| Comparative Negligence | Efficient | Efficient | ||
| Strict Liability w/Contributory Negligence | Efficient | Efficient |
Assuming all relevant standards of care are set at the efficient levels (xl=x∗)
Activity Levels under Negligence Rules
Contributory Negligence and Comparative negligence: efficient precaution by both parties
Leads injurer to take efficient precaution, so injurer expects to not be liable for any accidents
So Injurer ignores cost of accidents when deciding on activity level
- Drives carefully, but still drives too much
Victim bears residual risk
- Bikes carefully, and bikes efficient amount

Comparing Incentives Under Different Liability Rules
| Rule | Injurer Precaution | Victim Precaution | Injurer Activity | Victim Activity |
|---|---|---|---|---|
| No liability | Zero | Efficient | Too High | Efficient |
| Strict liability | Efficient | Zero | Efficient | Too High |
| (“Simple”) Negligence | Efficient | Efficient | Too High | Efficient |
| Negligence w/Contributory Negligence | Efficient | Efficient | Too High | Efficient |
| Comparative Negligence | Efficient | Efficient | Too High | Efficient |
| Strict Liability w/Contributory Negligence | Efficient | Efficient |
Assuming all relevant standards of care are set at the efficient levels (xl=x∗)
Activity Levels under Negligence Rules
Strict liability w/comparative negligence defense: if victim is not negligent, injurer is liable regardless of precaution
Leads both parties to take efficient precaution, so injurer is residual risk bearer, and is liable for any accidents
- So injurer weighs cost of accidents against benefits, drives efficient amount
Victim, fully insured, ignores cost of accidents when deciding on activity level
- Bikes carefully, but still bikes too much

Comparing Incentives Under Different Liability Rules
| Rule | Injurer Precaution | Victim Precaution | Injurer Activity | Victim Activity |
|---|---|---|---|---|
| No liability | Zero | Efficient | Too High | Efficient |
| Strict liability | Efficient | Zero | Efficient | Too High |
| (“Simple”) Negligence | Efficient | Efficient | Too High | Efficient |
| Negligence w/Contributory Negligence | Efficient | Efficient | Too High | Efficient |
| Comparative Negligence | Efficient | Efficient | Too High | Efficient |
| Strict Liability w/Contributory Negligence | Efficient | Efficient | Efficient | Too High |
Assuming all relevant standards of care are set at the efficient levels (xl=x∗)
Comparing Incentives Under Different Liability Rules
| Rule | Injurer Precaution | Victim Precaution | Injurer Activity | Victim Activity |
|---|---|---|---|---|
| No liability | Zero | Efficient | Too High | Efficient |
| Strict liability | Efficient | Zero | Efficient | Too High |
| (“Simple”) Negligence | Efficient | Efficient | Too High | Efficient |
| Negligence w/Contributory Negligence | Efficient | Efficient | Too High | Efficient |
| Comparative Negligence | Efficient | Efficient | Too High | Efficient |
| Strict Liability w/Contributory Negligence | Efficient | Efficient | Efficient | Too High |
Highlighted cases: party takes precaution only to AVOID liability ⟹ precaution is efficient, but activity level is too high
Comparing Incentives Under Different Liability Rules
| Rule | Injurer Precaution | Victim Precaution | Injurer Activity | Victim Activity |
|---|---|---|---|---|
| No liability | Zero | Efficient | Too High | Efficient |
| Strict liability | Efficient | Zero | Efficient | Too High |
| (“Simple”) Negligence | Efficient | Efficient | Too High | Efficient |
| Negligence w/Contributory Negligence | Efficient | Efficient | Too High | Efficient |
| Comparative Negligence | Efficient | Efficient | Too High | Efficient |
| Strict Liability w/Contributory Negligence | Efficient | Efficient | Efficient | Too High |
Highlighted cases: party reduces accidents, since they bear the cost, so both precaution & activity level are both efficient
These Results Look Overwhelming
| Rule | Injurer Precaution | Victim Precaution | Injurer Activity | Victim Activity |
|---|---|---|---|---|
| No liability | Zero | Efficient | Too High | Efficient |
| Strict liability | Efficient | Zero | Efficient | Too High |
| (“Simple”) Negligence | Efficient | Efficient | Too High | Efficient |
| Negligence w/Contributory Negligence | Efficient | Efficient | Too High | Efficient |
| Comparative Negligence | Efficient | Efficient | Too High | Efficient |
| Strict Liability w/Contributory Negligence | Efficient | Efficient | Efficient | Too High |
These results look overwhelming, but really the result of four basic ideas
These Results Look Overwhelming
| Rule | Injurer Precaution | Victim Precaution | Injurer Activity | Victim Activity |
|---|---|---|---|---|
| No liability | Zero | Too High | ||
| Strict liability | Zero | Too High | ||
| (“Simple”) Negligence | ||||
| Negligence w/Contributory Negligence | ||||
| Comparative Negligence | ||||
| Strict Liability w/Contributory Negligence |
1) If you don’t bear any of the cost of accidents, you have no incentive to prevent them
These Results Look Overwhelming
| Rule | Injurer Precaution | Victim Precaution | Injurer Activity | Victim Activity |
|---|---|---|---|---|
| No liability | Zero | Efficient | Too High | Efficient |
| Strict liability | Efficient | Zero | Efficient | Too High |
| (“Simple”) Negligence | ||||
| Negligence w/Contributory Negligence | ||||
| Comparative Negligence | ||||
| Strict Liability w/Contributory Negligence |
2) If you do bear the cost of accidents, you’ll do whatever you can to prevent them
These Results Look Overwhelming
| Rule | Injurer Precaution | Victim Precaution | Injurer Activity | Victim Activity |
|---|---|---|---|---|
| No liability | Zero | Efficient | Too High | Efficient |
| Strict liability | Efficient | Zero | Efficient | Too High |
| (“Simple”) Negligence | Efficient | Too High | ||
| Negligence w/Contributory Negligence | Efficient | Too High | ||
| Comparative Negligence | Efficient | Too High | ||
| Strict Liability w/Contributory Negligence | Efficient | Too High |
3) If you can avoid liability by exercising due care, you’ll do it, but then you won’t reduce activity
These Results Look Overwhelming
| Rule | Injurer Precaution | Victim Precaution | Injurer Activity | Victim Activity |
|---|---|---|---|---|
| No liability | Zero | Efficient | Too High | Efficient |
| Strict liability | Efficient | Zero | Efficient | Too High |
| (“Simple”) Negligence | Efficient | Efficient | Too High | Efficient |
| Negligence w/Contributory Negligence | Efficient | Efficient | Too High | Efficient |
| Comparative Negligence | Efficient | Efficient | Too High | Efficient |
| Strict Liability w/Contributory Negligence | Efficient | Efficient | Efficient | Too High |
4) If the other guy can duck liability with due care, you’re the residual risk bearer, and therefore you’ll take due care