3.2 — Efficient Breach

# 3.2 — Efficient Breach
## ECON 315 • Economics of the Law • Spring 2021
### Ryan Safner<br> Assistant Professor of Economics <br> <a href="mailto:safner@hood.edu"><i class="fa fa-paper-plane fa-fw"></i>safner@hood.edu</a> <br> <a href="https://github.com/ryansafner/lawS21"><i class="fa fa-github fa-fw"></i>ryansafner/lawS21</a><br> <a href="https://lawS21.classes.ryansafner.com"> <i class="fa fa-globe fa-fw"></i>lawS21.classes.ryansafner.com</a><br>

---

# Breach of Contract

---

# Breach of Contract

- ...what should happen when the promise is broken?

- .hi-green[Examples]:
  - I signed a contract with no intention of upholding it
  - or I signed it in good faith, intending to keep it
  - but circumstances changed, making my performance less desirable, maybe inefficient!
]
]
.pull-right[
.center[
![](../images/breach.jpg)
]
]

---

# Example

.quitesmall[
.bg-washed-green.b--dark-green.ba.bw2.br3.shadow-5.ph4.mt5[
- .hi-green[Example]: Consider a .blue[brewery] and an .red[ice company]. The .blue[brewery (buyer)] contracts to have the .red[ice company (seller)] deliver ice for storing beer.
]

- .red[Promisor]: ice company (seller)
- .blue[Promisee]: brewery (buyer)

- **V**: value of performance to .blue[promisee]
  - revenues from beer sold
- **C**: cost of performance to .red[promisor]
  - cost of supplying ice to brewery
- **P**: contract price buyer and seller agreed on
]

]

---

# Example

Lots of things could happen in between:

- Price of ice goes up, raising costs `$C>P$`
  - **efficient** to deliver, but .red[ice company] no longer wants to
- Or raises costs `$C>V$`
  - **no longer efficient** to deliver
- .purple[Another brewery] (with `$V'>V)$` could show up and offer the .red[ice company] `$P'>P$`
- Ice delivery person could break a leg, making it impossible to deliver
]
]
.pull-right[
.center[
![](../images/beer_ice.jpg)
]

]

---

# Breach of Contract

- .hi[Breach of contract] is when .red[promisor] fails to keep a promise
  - To make promise legally binding, must be some consequence to breach

- So what should happen when a contract is breached?
  - If penalty too small: law has no bite
  - If penalty too big: promises might be kept that are inefficient
  - .hi-purple[Can we design law to get breach only when it is efficient to breach?]
]
]
.pull-right[
.center[
![](../images/breach.jpg)
]
]

---

# Efficient Breach

|    |    |
|----|----|
| Buyer Payoff | `$V-P$`  (Buyer Surplus) |
| Seller Payoff | `$P-C$` (Seller Surplus) |
| Joint Payoff | `$V-C$`  (Gains from Trade) |

*Net gains* from the contract *performed*
]

- Suppose the cost of delivery `$C$` is uncertain when the contract is made

- Once the actual `$C$` is realized, .red[promisor (ice company)] must decide to **perform** or **breach** contract
  - `$C<V$`: efficient for .red[promisor] to **perform**
  - `$C>V$`: efficient for .red[promisor] to **breach**

---

# Efficient Breach

.smallest[
- Condition for .hi-purple[efficient performance]: `$C<V$`
  - .red[Promisor's cost to perform] `$<$` .blue[Promisee's benefit of performance]
  - Social benefit of breach `$<$` social cost of breach

- Condition for .hi-purple[efficient breach]: `$C>V$`
  - .red[Promisor's cost to perform] `$>$` .blue[Promisee's benefit of performance]
  - Social benefit of breach `$>$` social cost of breach
]
]
.pull-right[
.center[
![](../images/breach.jpg)
]
]

---

# What Will *Actually* Happen?

.pull-left[
.smallest[
- We know it's **efficient** to breach when `$C>V$`, but what will .red[promisor] **actually** do?
  - Depends only on their personal costs & benefits

- .red[Promisor]'s cost to perform `$<$` .red[promisor]'s liability from breach `$\implies$` .red[Promisor] will .hi-purple[perform]

- .red[Promisor]'s cost to perform `$>$` .red[promisor]'s liability from breach `$\implies$` .red[Promisor] will .hi-purple[breach]

]
]

---

# What Will *Actually* Happen?

- `$D$`: damages court awards to .blue[Promisee] (paid by .red[Promisor])

- .hi-turquoise[Promisor will perform]: `$-D>P-C$`

- .hi-turquoise[Promisor will breach]: `$-D<P-C$`

]

---

# What Will *Actually* Happen?

- `$D$`: damages court awards to .blue[Promisee] (paid by .red[Promisor])

- .hi-turquoise[Promisor will perform]: `$-D>P-C$`

- .hi-turquoise[Promisor will breach]: `$-D<P-C$`

- .hi-purple[Can we design the law to only get *efficient* breach of contract?]

]

---

# Getting Only Efficient Breach

- What value of `$D$` will equate the socially-optimal outcome and the .red[promisor's] private incentives to perform/breach?

`$$D=V-P$$`

- Set **liability from breach = .blue[promisee]'s net gain from performance**, then .red[promisor] will only breach when it is efficient
  - When .red[promisor] breaches, should owe penalty **exactly equal to** the benefit .blue[promisee] expected to recieve
  - This is .hi-purple[expectation damages]!

]

.pull-right[
|    |    |
|----|----|
| Buyer Payoff | `$V-P$`  (Buyer Surplus) |
| Seller Payoff | `$P-C$` (Seller Surplus) |
| Joint Payoff | `$V-C$`  (Gains from Trade) |

*Net gains* from the contract *performed*

]

---

# An Externalities View of Breach

.pull-left[
.smallest[
- If .red[Promisor] breaches contract, imposes a negative externality on .blue[Promisee]
  - .blue[Promisee] expected `$V-P$` payoff if .red[Promisee] performed
  - Under breach, .blue[Promisee] is `$V-P$` worse off

- If .red[Promisor] has to pay `$V-P$` in damages for breach, then .hi-purple[they internalize the externality]
  - Now .red[Promisor's] decision no longer affects .blue[Promisee's] payoff
  - Gets the same surplus whether or not contract is performed
  - With ext. internalized, .red[Promisor] chooses efficiently when deciding to *perform* or *breach*
]
]

---

# Reliance

---

# Return to Our Example

- **V**: value of performance to .blue[promisee]
  - revenues from beer sold
- **C**: cost of performance to .red[promisor]
  - cost of supplying ice to brewery
]

]

---
# Return to Our Example

.smallest[
.bg-washed-green.b--dark-green.ba.bw2.br3.shadow-5.ph4.mt5[
- .hi-green[Example]: Consider a brewery and an ice company. The brewery (buyer) contracts to have the ice company (seller) deliver ice for storing beer.
]
- Suppose the two companies agree on a price `$P$` and the .red[ice company] *expects* `$\mathbb{E}[C]<P$`

- Then both parties can expect to benefit from performance:
`$$V>P>\mathbb{E}[C]$$`

]

---

# Reliance

.pull-left[
.smallest[
- Suppose that in preparation for sale, the .blue[brewery] invests `$R$` in producing a certain amount of beer, prior to the ice actually being delivered

- This is a .hi[reliance investment], which depends on the performance of the contract
  - .hi-purple[Increases the value of performance] to .blue[promisee]
  - .hi-purple[Increases the social cost of breach]

- Another goal of contract law is to attain .hi-purple[optimal level of reliance]
]
]

---

# Reliance: Example

- `$V$` depends on the value of `$R$`
  - More `$R$` makes `$V$` higher to promisee

- But must choose `$R$` *before* contract is performed/breached (ice delivered or not) and is a .hi[sunk cost] (beer will spoil if ice not delivered)

]

---

# Reliance: Example

- `$D$`: damages the court awards in the event of breach (promisor pays promisee)

- What value of `$D$` is efficient, i.e. induces promisor to breach only when it is efficient to do so?

]

---

# Breach

| Payoffs | Performance | Breach |
|---------|-------------|--------|
| Buyer's Payoff | `$V-P$` | `$D$` |
| Seller's Payoff | `$P-C$` | `$-D$` |
| Joint Payoff | `$V-C$` | `$0$` |

---

# Breach with Reliance

| Payoffs | Performance | Breach |
|---------|-------------|--------|
| Buyer's Payoff | `$V-R-P$` | `$D-R$` |
| Seller's Payoff | `$P-C$` | `$-D$` |
| Joint Payoff | `$V-R-C$` | `$-R$` |

- Recall condition for efficient breach: `$\color{#6A5ACD}{C>V}$`
  - cost of performance to .red[promisor] `$>$` value of performance to .blue[promisee]

- Note since `$R$` is a sunk cost, doesn't affect this condition!
  - Joint payoff from performance `$>$` joint payoff from breach if: `$V-R-C>-R$`
  - `$R$`'s cancel, yielding `$\color{#6A5ACD}{C>V}$`

---

# Reliance: Example

| Payoffs | Performance | Breach |
|---------|-------------|--------|
| Buyer's Payoff | `$V-R-P$` | `$D-R$` |
| Seller's Payoff | `$P-C$` | `$-D$` |
| Joint Payoff | `$V-R-C$` | `$-R$` |

- Now consider what Seller will *actually* choose to do (once it knows `$C)$`:

- .hi-purple[Seller will breach when] `$$\color{#6A5ACD}{C>P+D}$$`
  - Left: benefit of breach (savings in cost)
  - Right: cost of breach (lost price plus damages)
  - Breaches when private benefits `$>$` private costs

---

# Reliance: Example

| Payoffs | Performance | Breach |
|---------|-------------|--------|
| Buyer's Payoff | `$V-R-P$` | `$D-R$` |
| Seller's Payoff | `$P-C$` | `$-D$` |
| Joint Payoff | `$V-R-C$` | `$-R$` |

- We want law to incentivize seller to breach only when it is efficient
  - So set `$C>P+D$` equal to `$C>V$`, i.e.
  - .hi-purple[Set damages] `$\color{#6A5ACD}{D=V-P}$`.hi-purple[, equal to consumer surplus]
  - Seller compensates buyer for the buyer's lost surplus from the exchange

---

# What Do Courts Set Damages At?

- We know what damages induce efficient breach `$(D=V-P)$`, but what damages do courts **actually** set in breach cases?

- .hi[Expectation damages]: amount to make the promisor as well off .hi-purple[as if the contract had been performed]
  - by far the most popular method
  - We've seen this induces breach only when it's efficient ✅

]

.pull-right[
| Payoffs | Performance | Breach |
|---------|-------------|--------|
| Buyer's Payoff | `$V-R-P$` | `$D-R$` |
| Seller's Payoff | `$P-C$` | `$-D$` |
| Joint Payoff | `$V-R-C$` | `$-R$` |

]

---

# What Do Courts Set Damages At?

.pull-left[
- .hi[Reliance damages]: amount to make the promisor as well off .hi-purple[as if the contract had never been made]
  - reference point is *pre-contract* status, rather than *post-performance* status
  - buyer's pre-contract payoff was 0, so in breach case, set `$D=R$`

]

---

# What Do Courts Set Damages At?

- Recall seller will *want* to breach when `$C>P+D$`
  - If `$D=R$`, then:

- .hi-purple[Seller will want to breach when] `$\color{#6A5ACD}{C>P+R}$`
  - Since `$V-P>R$` (.blue[promisee]'s reliance investment must be less than the gain from performance, otherwise unprofitable to invest!)...,
  - Then `$P+R<V$`, implying .hi-purple[seller will breach too often under reliance damages] (since `$C<V$` is inefficient to breach) 
  
]
]

]

---

# What Do Courts Set Damages At?

- Finally, consider a rule of no damages `$(D=0)$`

- .red[Promisor] will want to breach whenever `$C>P$`
  - Will want to breach **even more often** than reliance (or expectation) damages
  - Recall it's only efficient to breach when `$C>V$`, and `$V>P$`
]

---

# What Do Courts Set Damages At?

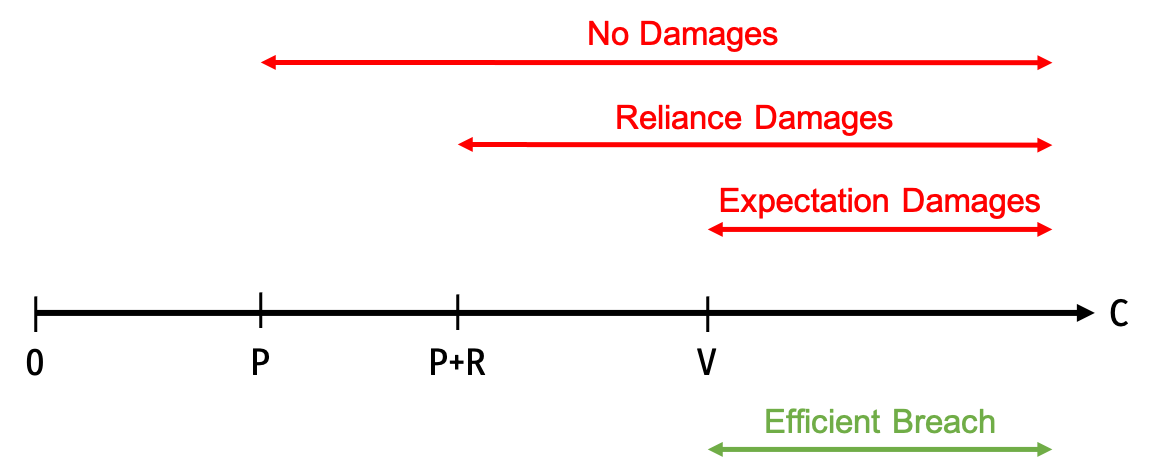
Ranges of production costs over which breach occurs under the various damage measures

]

---

# An Example

.smallest[
.bg-washed-green.b--dark-green.ba.bw2.br3.shadow-5.ph4.mt5[
- .hi-green[Example]: I am an aircraft manufacturer, you and I sign a contract
  - You agree to pay me $350,000
  - I agree to deliver an airplane to you
  - You value the airplane at $500,000
  - I expect it will cost me $300,000 to produce
]
]
]

---

# An Example

- If contract is performed:

| Party |    | Payoff |
|-----|----|----:|
| You | V-P = | $150,000 |
| Me | P-C = | $50,000 |
| **Joint** | V-C = | **$200,000** |
]
]

]

---

# An Example

.quitesmall[
- Suppose my costs rise to $400,000
  - I don't want to perform `$(P<C')$`
  - But efficient to perform `$(C'<V)$`

- If contract is performed:

| Party |    | Payoff |
|-----|----|---:|
| You | V-P = |$150,000 |
| Me | P-C' = | -$50,000 |
| **Joint** | V-C' = | **$100,000** |

]
]

]

---

# An Example

.quitesmall[
- Suppose my costs rise to $400,000
  - I don't want to perform `$(P<C')$`
  - But efficient to perform `$(C'<V)$`

- Under .hi[expectation damages]: I would owe you $150,000
  - Since `$D<P-C'$`, I'll perform (better to lose only $50,000!)
  - .hi-turquoise[Efficient performance], since `$C'<V$`!
  
| Party |    | Payoff |
|-----|----|---:|
| You | V-P = | $150,000 |
| Me | P-C' = | -$50,000 |
| **Joint** | V-C' = | **$100,000** |

]
]

]

---

# An Example

.quitesmall[
- Suppose my costs rise to **$600,000**
  - I don't want to perform `$(P<C'')$`
  - Efficient to not perform `$(C''>V)$`

- If contract is performed:

| Party |    | Payoff |
|-----|----|---:|
| You | V-P = | $150,000 |
| Me | P-C'' = | -$250,000 |
| **Joint** | V-C'' = | **-$100,000** |

]
]

---

# An Example

- Suppose my costs rise to **$600,000**
  - I don't want to perform `$(P<C'')$`
  - Efficient to not perform `$(C''<V)$`

- Under .hi[expectation damages]: I would owe you $150,000
  - Since `$D>P-C''$`, I will breach (better to lose only -$150,000)
  - .hi-turquoise[Efficient breach], since `$C''>V$`!

| Party |    | Payoff |
|-----|----|---:|
| You | D = | $150,000 |
| Me | -D = | -$150,000 |
| **Joint** | D-D = | **$0** |

]
]

---

# An Example with Reliance

.quitesmall[
.bg-washed-green.b--dark-green.ba.bw2.br3.shadow-5.ph4.mt5[
- .hi-green[Example]: I am an aircraft manufacturer, you and I sign a contract
  - You agree to pay me $350,000
  - I agree to deliver an airplane to you
  - You value the airplane at $500,000
  - I expect it will cost me **$300,000** to produce
  - .hi-turquoise[You buy a $75,000 hangar that increases the value of performance to $600,000]
]

]
]

.smallest[
- V': **$600,000**
- P: $350,000
- .hi-turquoise[R: $75,000]
- C: **$300,000**
- .red[D: ?]
]

]

---

# An Example with Reliance

- With your .hi[reliance investment] in the hangar, If I breach the contract, should I owe...
  - $150,000? (V-P, value of original promise)
  - $175,000? (V'-P, value of performance after your investment)
  - $225,000? (V-P+R, value of original promise plus your reliance investment)
]
]

.smallest[
- V': **$600,000**
- P: $350,000
- .hi-turquoise[R: $75,000]
- C: **$300,000**
- .red[D: ?]
]

]

---

# An Example with Reliance

.smaller[
- To get .hi-purple[efficient breach] only, damages must include the .hi-purple[added benefit] from reliance
  - You anticipate benefit (with hangar) of $175,000 `$(V'-P-R)$`
  - If `$D>175,000$`, I will breach too often (any time `$C > P$`, rather than only when `$C > V)$`
]
]

.smallest[
- V': **$600,000**
- P: $350,000
- .hi-turquoise[R: $75,000]
- C: **$300,000**
- .red[D: ?]
]
]

---

# An Example with Reliance

- But this affects .blue[your] incentives about *how much* to rely on .red[my performance]; .blue[your payoffs] if:
  - .blue[No hangar] and .red[I perform]: **$150,000** (500,000-350,000)
  - .blue[No hangar] and .red[I breach] (with .hi[expectation damages]): **$150,000**
  - .blue[Hangar] and .red[I perform]: **$175,000** (600,000-350,000-75,000)
  - .blue[Hangar] and .red[I breach] (with .hi[expectation damages] that include the full amount): **$175,000**

- So if .hi[expectation damages] include the *full* added benefit, .hi-purple[promisee will over-rely!]
]
]

.smallest[
- V': **$600,000**
- P: $350,000
- .hi-turquoise[R: $75,000]
- C: **$300,000**
- .red[D: ?]
]
]

---

# Expectation Damages and Overreliance

- So if .hi[expectation damages] include the *full* added benefit, .hi-purple[promisee will over-rely!]

- Creates a .hi[moral hazard problem]
  - .blue[Promisee] inefficiently over-invests in reliance
  - Expectation damages fully insure buyer against risk of breach, behaves as if performance were certain
  - .blue[Promisee] has no incentive to take precautions against possibility of breach
]
]

---

# Reliance and Breach

- If damages *include* full added benefit from reliance, .blue[promisee] will invest more than the efficient amount in reliance

- But if damages *exclude* the added benefit, then .red[promisor] will breach more often than is efficient, and underinvest in performance
  - .red[Promisor]'s liability < .blue[Promisee]'s benefit from performance
  - `$D<(V'-P)$`

]

---

# Reliance and Breach

- .hi[Paradox of compensation]: a single “price” (damages owed) sets multiple incentives
  - How much the .red[promisor] will invest in performance, whether or not to breach or perform
  - How much the .blue[promisee] will invest in reliance
  - Impossible to set them all efficiently!

]

---

# Efficient Reliance

.pull-left[
.smaller[
- Cooter & Ulen: include only .hi-purple[efficient reliance]
  - .hi[Perfect expectation damages]: restore .blue[promisee] to level of well-being she would have gotten from performance .hi-purple[if she had relied the efficient amount]
  - .blue[Promisee] rewarded for efficient reliance, not overreliance

- Actual courts: include only .hi[forseeable] reliance
  - How much .red[promisor] could **reasonably expect** .blue[promisee] to rely
]
]

---

# Forseeable Reliance: Hadley v. Baxendale

- *Hadley v. Baxendale* (1854) EWHC J70

- Hadley owned a flour mill, crankshaft broke

- Hired Baxendale to transport broken shaft for repair
  - Baxendale shipped by boat instead of by train, causing a delay of a week

- Hadley sued Baxendale for week of lost profits

]
.pull-right[
.center[
![](../images/mill.png)
]
]

---

# Overreliance

- *Hadley v. Baxendale* (1854) EWHC J70

- Defendant conceded negligence in delaying the delivery, but claimed the requested damages were too high, since the need for the mill to close was only a “remote” possibility

> “The shipper assumed that Hadley, like most millers, kept a spare shaft...Hadley did not inform him of the special urgency in getting the shaft repaired.”

]
.pull-right[
.center[
![](../images/mill.png)
]
]

---

# Hadley v. Baxendale

- Court elucidated the following rule:

.quitesmall[
> “Where two parties have made a contract which one of them has broken, the damages which the other party ought to recieve in respect of such breach of contract should be such as may fairly and reasonably be considered either arising naturally, i.e., according to the usual course of things, from such breach of contract itself, or such as may reasonably be supposed to have been in the conemplation of both parties, at the time they made the contract, as the probable results of the breach of it.”

]

]

---

# Hadley v. Baxendale

- *Hadley v. Baxendale* (1854) EWHC J70

- In other words, expectation damages for breach will be .hi[limited] to a .hi[reasonable] level
  - What the parties could have .hi-purple[reasonably foreseen] at the time they made the contract
  - And liable for .hi-purple[no more] than that

- Found the lost profits were not reasonably forseeable, thus not entitled to damages on those

]

---

# Hadley v. Baxendale

.quitesmall[
> “But it is obvious that, in the great multitude of cases of millers sending off broken shafts to third persons by a carrier under ordinary circumstances, [these particular] consequences would not, in all probability, have occurred, and these special circumstances were here never communicated by the plaintiffs to the defendants. It follows, therefore, that the loss of profits here cannot reasonably be considered such a consequence of the breach of contract as could have been fairly and reasonably contemplated by both the parties when they made this contract”

]

]

---

# Reasonably Forseeable Reliance

---

# Default Rules

---

# Forseeable Reliance

- Why didn’t Hadley and Baxendale just specify in the original contract what happens in the event of a delay?

- What rules should apply in circumstances that *aren’t* specified in a contract?
]

---

# Complete Contracts

- In economics & contract theory, a .hi[complete contract] specifies all actions or transfers that parties must take under every possible contingency

- In the real world of .hi-purple[uncertainty], complete contracts are impossible

- Instead people maximize their *expected* utility given limited information at the time (.hi-purple[“bounded rationality”])

]

---

# Consequences of Incomplete Contracts

- Agreements are always .hi[incomplete contracts], actions for many (unforeseen) contingencies are *unspecified*

- Even for *specified* actions and contingences, outcomes are indeterminate due to .hi-purple[enforcement costs]
  - argument about interpretation
  - slow litigation process, legal fees

- Gives rise to .hi-purple[post-contractual opportunism] (shirking, fraud, renegotiation, hold-up, etc)
]

---

# I Am Altering The Deal...

]

---

# ...Pray I Don't Alter it Any Futher

.center[
<iframe width="980" height="550" src="https://www.youtube.com/embed/OXyH1XkQo44" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>
]

---

# Asides: I/O & Theory of Firm

[ECON 326 — Industrial Organization](https://ios20.classes.ryansafner.com)
]
]

.pull-right[
.smallest[
- Research in industrial organization about how .hi-purple[firms solve these problems of transaction costs]
  - vertical integration to prevent post-contractual opportunism
  - contractual restraints (that look like they create market power but are actually efficient)

- Note this line of research comes directly out of Coase (1937): firms are a solution to high transaction cost situations
  - Coase (1960): the law is another
]
]

---

# Firm as Owner of Residual Control Rights

1948-

Economics Nobel 2016
]
]
]

.right-column[
.smaller[
> ".hi[We define the firm as being composed of the assets (e.g., machines, inventories) that it owns.] We present a theory of .hi[costly contracts] that emphasizes that .hi[contractual rights can be of two types: specific rights and residual rights.] When it is too costly for one party to specify a long list of the particular rights it desires over another party's assets, .hi[it may be optimal for that party to purchase all the rights except those specifically mentioned in the contract. Ownership is the purchase of these residual rights of control.]" (p.692).

]
]

.source[Hart, Oliver and Sanford J Grossman, 1986, "The Costs and Benefits of Ownership: A Theory of Vertical and Lateral Integration," *Journal of Political Economy* 94(4): 691-719]

---

# Default Rules

- .hi-purple[Gaps] in contracts: risks or circumstances not explicitly addressed
  - (In a world of no transaction costs, parties could specify all possible contingencies, nothing left unclear)
  - Can be inadvertent or deliberate

- .hi[Default rules]: the rules courts apply to fill in gaps
]

# How Much Should We Write Into a Contract?

- Better to include a contingency in a contract or leave it a gap?
  - Allocating a .hi-purple[risk] *ex ante* before it becomes a loss for someone
  - Versus allocating a .hi-purple[loss] *ex post*
    - Only have to deal with this if it actually occurs
]

---

# What Should the Default Rules Be?

.smallest[
- Cooter & Ulen: use the rule parties would have wanted .hi-purple[if they had chosen] to bargain over this issue
  - this will be whatever rule is efficient

- .hi-purple[Normative Coase Theorem] implies law should minimize transaction costs
  - filling a gap requires some cost, so use the rule the parties *would have wanted* had they hashed it out
  - that way, most contracts can just rely on the default rule rather than hash it out
]
]

---

# What Should the Default Rules Be?

- Don’t want ambiguity in law, so default rule can’t be different case by case

- .hi-purple[Majoritarian default rule]: the terms that most parties would agree to
  - In cases where rule is not efficient, parties can still agree to override it in their contract

- Court: figure out .hi-purple[efficient allocation of risks] (what parties would have done)
]

---

# Default Rules: Example

.pull-left[
.smallest[
.bg-washed-green.b--dark-green.ba.bw2.br3.shadow-5.ph4.mt5[
- Suppose a family contracts with construction company to build house

- Construction company knows: 50% chance of costs increasing by $2,000
  - In expected value, costs will be $1,000 higher due to this risk

- The company can hedge this risk (buy supplies in advance and keep in storage, etc.) at a cost of $400

- Family doesn’t know anything about this possibility, and has no way to mitigate the risk
]
]

]

---

# Default Rules: Example

- The company chooses not to hedge against the risk

- It turns out, costs indeed went up $2,000
  - Company raises the price on the family ($2,000), family refuses to pay, case goes to court

- **How should the court address this?**
  - Original contract says nothing about the risk of higher construction costs
]

---

# Default Rules: Example

- Construction company here is the .hi-purple[efficient bearer] of the risk
  - Cost to family was $1,000 in expected value, no way to mitigate
  - Company could have mitigated it for $400

- An efficient contract would have allocated the risk to the company

]

---

# Default Rules: Example

- Court might rule the spike in costs was reasonably forseeable
  - If forseeable, safe to assume already incorporated in price (compensating company for bearing risk)

- It might *not* have been reasonably forseeable
  - Company might still be efficient bearer of risk, but not part of price (unforseen risk)
  - Court might rule for the family, but have them pay a different price to compensate Company for the risk
]
]

---

# Default Rules: Penalty Default

.pull-left[
.smaller[
- Sometimes better to make default rules something the parties .hi-purple[would not have wanted], a .hi[penalty default]
  - Gives an incentive for parties to address the issue rather than leave a gap
  - Incentive to disclose information

- Ayres & Gertner argue sometimes gaps are result not of transaction costs, but strategic reasons
  - holdout problems, asymmetric information
]

.source[Ayres, Ian and Robert Gertner, 1989, “Filling Gaps in Incomplete Contracts: An Economic Theory of Default Rules,” *Yale Law Journal* 99]
]

---

# Hadley v. Baxendale Rule: Penalty Default?

- Baxendale (shipper) is only one who can affect when crankshaft is delivered — efficient bearer of risk
  - It was his decision to ship via a slower method which hurt Hadley’s profits
  - If Baxendale were liable, he would have internalized this external cost

- If default rule held Baxendale liable, Hadley has no need to tell him the shipment is urgent!
  - Which he didn’t, and so Baxendale inadvertently chose a less efficient shipping method

- So Hadley might conceal this information, which is inefficient
]

---

# Hadley v. Baxendale Rule: Penalty Default?

- Ayres and Gernet: Hadley vs. Baxendale ruling was correct, not because it was efficient, but **because it was inefficient!**

- Ruling created incentive for disclosing information and forcing parties to prevent inefficient gaps in contracts
]

---

# Hadley v. Baxendale Rule: Penalty Default?

.pull-left[
.quitesmall[
- To see their logic, suppose
  - 80% of millers are **low damage** — suffer $100 loss in delay
  - 20% of millers are **high damages** — suffer $200 loss in delay

- If shipper is liable for .hi-turquoise[actual damages]
  - Average miller would suffer $120 in losses
  - Shipper makes efficient investment for average miller
  - But not efficient for either type

- If shipper is liable for .hi-turquoise[forseeable damages] (Hadley rule)
  - Shipper makes efficient investment for low-damage millers
  - High-damage millers have strong incentive to negotiate around default rule
]
]

---

# When To Use Penalty Defaults

- Look at why parties left a gap in a contract:

- If due to high transaction costs `$\rightarrow$` use efficient rule

- If due to strategic reasons `$\rightarrow$` penalty default may be more efficient
]